米蘭牛角尖

啊！好久沒有實作了，不曉得各位還記不記得怎麼寫 Python 呢？今天的這篇文章將主要以實作為主，簡單地介紹如何搭建出我們在過去幾天的旅程中，學到的那些形形色色的深度學習模型：LSTM、GRU，以及兩者的雙向版本，也就是BiLSTM、以及BiGRU。不過，你可能已經發現，咦？那單純的 RNN 呢？事實上，在自然語言處理的實務中，由於先前提過的那些缺失，如記性不好等問題，已經很少人使用單純的 RNN 來完成任務了。欸！別人都是一篇一個神經網路，我直接一篇全部寫完，超值吧！還不趕快再點一下我其他文章！

不過在開始弄髒你的手實際上工之前，我們得先了解今天要用的工具有哪些。

今天要使用的工具箱

對於一些可能從未寫過程式的朋友，可能會有一些疑慮，擔心說「我們該不會要從零開始搭神經網路吧？先前介紹過的那些輸出層、輸入層、隱藏層殺毀的，我們都要從頭開始做起嗎？別吧？」接著擺出了 No No No 的手勢。

事實上，像這種這麼常用的深度學習工具，不可能沒有前人寫過。所謂前人種樹，後人乘涼，在過去就已經有程式大神代替我們將這些深度學習以及神經網路整理成 API 了。什麼？你說什麼是API？沒事，你只需要理解因為某邪惡大神的建樹，我們只需要簡單地引入（import）工具箱後，這些神經網路就可以隨取隨用了。我想，最多只需要調參數、以及疊各種隱藏層吧？而我今天就會一步一步地仔細帶領你撰寫搭建模型的程式，並逐句介紹這些程式語言在做什麼。至於是哪個大神如此邪惡，擁有幾乎全世界所有網頁的資料，又有極大量的運算資源？其實也沒有別人了，就是：

Tensorflow

Tensorflow 是一個開源的深度學習程式庫，並利用機器學習來完成各種人工智慧的下游任務，例如：圖像辨識，還有我們的重點，自然語言處理。你現在所用的幾乎所有 Google 的服務，舉凡如 Google 搜尋、Google 翻譯（乙定要有的吧！）、GOogle 語音辨識、Google 地圖、Google 相片，都是來自於利用 Tensorflow 的深度學習框架所打造而成的。換句話說，我們其實就是站在 Google 打造好的立足點來解決自然語言處理的應用。

LSTM

首先，在程式檔的頂端，我們得先引用搭建神經網路所需要的工具箱，也就是 Tensorflow。今天，我們會直接使用 tensorflow 內建的 imdb 資料集。資料科學的前輩對imdb資料一定又愛又恨吧！

1
2
3
4
5
6
7
8
9

import tensorflow as tf
from tensorflow.keras.datasets import imdb # 引入資料集
from tensorflow.keras.models import Sequential # 引入序列模型，記得我們在先前提到的 sequence model嗎？
from tensorflow.keras.layers import Dense # 一層全連接的神經網路
from tensorflow.keras.layers import LSTM # 長短期記憶（Long Short-term memory）
from tensorflow.keras.layers import Embedding # 使模型理解語意的 Embedding
from tensorflow.keras.preprocessing import sequence 
# 在前處理會需要用到，將長短不一的資料補齊或截斷成相同長度（記得我們先前所說神經網路的長度可以彈性調整嗎？就是透過這裡將序列轉換成相同長度）
tf.random.set_seed(7)  # 設定隨機種子

再來得將資料先處理好，我們在這邊先將資料處理好之後，後續在搭建無論是 GRU，甚至是BiLSTM、BiGRU，都會直接用這裡的資料，就不會再重複這裡的動作啦！

1
2
3
4
5
6
7
8

# 設定資料中字頻前五千的字
top_words = 5000 
# 取得資料後，分成訓練資料集以及測試資料集
(X_train, y_train), (X_test, y_test) = imdb.load_data(num_words=top_words) 
# 在這裡就是要截斷或補齊輸入模型的句子，以保持所有句子長度相同。
max_review_length = 500
X_train = sequence.pad_sequences(X_train, maxlen=max_review_length)
X_test = sequence.pad_sequences(X_test, maxlen=max_review_length)

接著要先搭建模型，搭建完模型之後才會開始訓練。

1
2
3
4
5
6
7
8
9
10
11
12
13

embedding_vector_length = 32
# 首先設定模型為序列模型
lstm_model = Sequential()
# 將已經訓練好的 Embedding 加入神經網路模型中
lstm_model.add(Embedding(top_words, embedding_vector_length, input_length=max_review_length))
# LSTM函數中的值則是代表你要在模型中放入多少 LSTM 的神經元（有門閥的那個）
lstm_model.add(LSTM(100))
# 全連接的神經網路隱藏層，可以選擇想要的激勵函數
lstm_model.add(Dense(1, activation='sigmoid'))
# 這裡的compile是在將模型組合起來。
lstm_model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# 可以一起來看看模型長怎樣
print(lstm_model.summary())

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 embedding (Embedding)       (None, 500, 32)           160000    
                                                                 
 lstm (LSTM)                 (None, 100)               53200     
                                                                 
 dense (Dense)               (None, 1)                 101       
                                                                 
=================================================================
Total params: 213,301
Trainable params: 213,301
Non-trainable params: 0
_________________________________________________________________
None

我們從params中可以看到模型總共有多少個參數。另外，在 LSTM 中的參數決定的是神經元數量，沒有一定的固定數字，但是有個模式可循。首先，RNN 的寬度代表特徵的多寡，由輸入以及篩選器的數量決定；深度代表的則是特徵的豐富度，由神經網路層數及步驟數決定的。若不需要從原資料產出大量特徵，那麼一般來說寬度會減少。若資料相對單純，那麼深度則需要調整的淺一點，這麼做可以節省訓練時間及資源。(source)

確認沒問題之後，就可以開始訓練模型了！這裡可能會需要跑比較久時間，像我試跑就跑了十分多鐘，所以才說深度學習模型的一個缺點就是速度比較慢一點。

1
2
3

model.fit(X_train, y_train, epochs=3, batch_size=64) # 訓練模型
scores = model.evaluate(X_test, y_test, verbose=0) # 測試模型
print("Accuracy: %.2f%%" % (scores[1]*100)) 

1
2
3
4
5
6
7

Epoch 1/3
391/391 [==============================] - 207s 525ms/step - loss: 0.4316 - accuracy: 0.7884
Epoch 2/3
391/391 [==============================] - 205s 525ms/step - loss: 0.2653 - accuracy: 0.8937
Epoch 3/3
391/391 [==============================] - 204s 522ms/step - loss: 0.2377 - accuracy: 0.9065
Accuracy: 86.72%

BiLSTM

其實雙向的 BiLSTM 也是大同小異，我們只需要關注模型的搭建上就可以了。資料一樣沿用在上面所整理好的訓練以及測試資料集。別忘了要先引進雙向的套件，至於其他的套件，在前面就已經引進過，就不需要再引進了。

1

from tensorflow.keras.layers import Bidirectional

1
2
3
4
5
6

bilstm_model = Sequential()
bilstm_model.add(Embedding(top_words, embedding_vetcor_length, input_length=max_review_length))
bilstm_model.add(Bidirectional(LSTM(100, dropout=0.2, recurrent_dropout=0.2)))
bilstm_model.add(Dense(1, activation='sigmoid'))
bilstm_model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(bilstm_model.summary()) # 同樣先來看模型參數

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

Model: "sequential_1"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 embedding_1 (Embedding)     (None, 500, 32)           160000    
                                                                 
 bidirectional (Bidirectiona  (None, 200)              106400    
 l)                                                              
                                                                 
 dense_1 (Dense)             (None, 1)                 201       
                                                                 
=================================================================
Total params: 266,601
Trainable params: 266,601
Non-trainable params: 0
_________________________________________________________________
None

1
2
3

bilstm_model.fit(X_train, y_train, epochs=3, batch_size=64)
scores = bilstm_model.evaluate(X_test, y_test, verbose=0)
print("Accuracy: %.2f%%" % (scores[1]*100))

1
2
3
4
5
6
7

Epoch 1/3
391/391 [==============================] - 805s 2s/step - loss: 0.4870 - accuracy: 0.7579
Epoch 2/3
391/391 [==============================] - 803s 2s/step - loss: 0.3148 - accuracy: 0.8726
Epoch 3/3
391/391 [==============================] - 799s 2s/step - loss: 0.2637 - accuracy: 0.8944
Accuracy: 87.89%

BiLSTM 因為參數更多，所以訓練時間又很明顯地變更久了。我在這裡花了快20多分鐘在訓練模型。

GRU

1
2
3
4
5
6
7

gru_model = Sequential()
gru_model.add(Embedding(top_words, embedding_vector_length, input_length=max_review_length))
gru_model.add(GRU(32))
gru_model.add(Dense(10, activation='relu'))
gru_model.add(Dense(1, activation='sigmoid'))
gru_model.compile(loss="binary_crossentropy", optimizer='adam',metrics=['accuracy'])
print(gru_model.summary())

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

Model: "sequential_2"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 embedding_2 (Embedding)     (None, 500, 32)           160000    
                                                                 
 gru (GRU)                   (None, 32)                6336      
                                                                 
 dense_2 (Dense)             (None, 10)                330       
                                                                 
 dense_3 (Dense)             (None, 1)                 11        
                                                                 
=================================================================
Total params: 166,677
Trainable params: 166,677
Non-trainable params: 0
_________________________________________________________________

1
2
3

gru_model.fit(X_train, y_train, epochs=3, batch_size=64)
scores = gru_model.evaluate(X_test, y_test, verbose=0)
print("Accuracy: %.2f%%" % (scores[1]*100))

1
2
3
4
5
6
7

Epoch 1/3
391/391 [==============================] - 89s 222ms/step - loss: 0.4658 - accuracy: 0.7620
Epoch 2/3
391/391 [==============================] - 88s 226ms/step - loss: 0.2631 - accuracy: 0.8943
Epoch 3/3
391/391 [==============================] - 88s 224ms/step - loss: 0.2215 - accuracy: 0.9149
Accuracy: 87.74%

GRU 模型當初有說，其實設計架構上與 LSTM 差不了多少，但是由於 GRU 的參數相對比較少的緣故，所以運算時間還有資源都比原本的 LSTM 還要少。在準確度皆為接近 90% 的前提下，我在前面訓練 LSTM 的時間為十一分鐘左右，而這裡 GRU 我卻只需要五分多鐘就結束訓練了。

1
2
3
4
5
6
7

bigru_model = Sequential()
bigru_model.add(Embedding(top_words, embedding_vector_length, input_length=max_review_length))
bigru_model.add(Bidirectional(GRU(32)))
bigru_model.add(Dense(10, activation='relu'))
bigru_model.add(Dense(1, activation='sigmoid'))
bigru_model.compile(loss="binary_crossentropy", optimizer='adam',metrics=['accuracy'])
bigru_model.summary()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

Model: "sequential_3"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 embedding_3 (Embedding)     (None, 500, 32)           160000    
                                                                 
 bidirectional_1 (Bidirectio  (None, 64)               12672     
 nal)                                                            
                                                                 
 dense_4 (Dense)             (None, 10)                650       
                                                                 
 dense_5 (Dense)             (None, 1)                 11        
                                                                 
=================================================================
Total params: 173,333
Trainable params: 173,333
Non-trainable params: 0
_________________________________________________________________

1
2
3

bigru_model.fit(X_train, y_train, epochs=3, batch_size=64)
scores = bigru_model.evaluate(X_test, y_test, verbose=0)
print("Accuracy: %.2f%%" % (scores[1]*100))

1
2
3
4
5
6
7

Epoch 1/3
391/391 [==============================] - 166s 414ms/step - loss: 0.4397 - accuracy: 0.7790
Epoch 2/3
391/391 [==============================] - 160s 408ms/step - loss: 0.2599 - accuracy: 0.8975
Epoch 3/3
391/391 [==============================] - 159s 407ms/step - loss: 0.2170 - accuracy: 0.9153
Accuracy: 87.74%

BiGRU 的模型訓練時間跟 BiLSTM 相比就更明顯了，BiLSTM 我當初花了 40 分鐘左右才訓練完成，反觀 BiGRU，只需要 9 分鐘左右就結束了，模型表現卻也都差不多。

結語

我們最後來看一下結果，可以發現四種表現都沒有差距太大，但訓練時間就有明顯的差異，也就是 GRU 的時間還要少於 LSTM；另外，雙向的神經網路模型表現也比單向還要好一些。

這也印證了在先前 【NLP】Day 17: 每天成為更好的自己！神經網路也是！深度學習模型 GRU 的文章中所說，參數的多寡會大大影響著運算時間以及資源。好，神經網路的實作就到這邊，是不是比想像中的還要簡單很多呢？明天開始就要進入 BERT 了喔！

空頭不死，多頭不止；多頭不死，空頭不止
不詳

在股票市場中，人人著稱的一句話：「空頭不死，多頭不止；多頭不死，空頭不止。」意思是，如果股價在下降的趨勢時中，如果想一直有抄底，期望做反彈的人不斷進場的話，那麼市場就會不斷下跌。我想我在這裡可以再多加一句：

單頭一有，強到流油；注意多頭，更上層樓！
By me

只是差別是，一個在講的是股市走向及股民心理，另一個則是在講 Attention Is All You Need 論文的 Transformer 模型，以及在其中所運用的自注意力機制（Self-attention Mechanism）。昨天的文章中，我們已經簡單地了解何謂自注意力機制。在同一篇文章中，作者又針對這個自注意力機制再次進行了改良 完全不給其他人優化的機會喔，也就是將原本提出的單一自注意力機制，在模型中改良成多頭自注意力機制（Multi-head Self-attention Mechanism）。今天，就讓我們一起來看看 Multi-head Self-Attention Mechanism 跟原本的有什麼不一樣呢？接著，再把剩下的 Encoder 以及 Decoder 走完吧！

Multi-head Self-attention Mechanism

若你還記得的話，在昨天的文章，【NLP】Day 19: 注意！謝謝你的注意！Transformer （上）之中，曾經提到 Transformer 會將每一個字的向量（也就是Word-embedding）乘上一個權重 之後，會得到三個不同的向量，分別是 、 以及 ，也就是 queue vector、key vector，以及value vector。那 Multi-head Self-attention Mechanism 其實就是不同的字要乘上不同的權重 ，也就是說，不同的字會有不同的、 以及 。我們可以先看看下圖：

在這邊再強調一次，這邊的 、 以及 三個向量，是 分別與 、
以及 內積所得的結果。有幾個維度，就有幾個 Head；同理，若訓練資料的 Word Embedding 總共有 8 個維度，那麼就會有 8 個不同的 Head。最後我們就會得到 8 個 的矩陣。 但是問題在於，接下來要將資料餵入的模型事前饋神經網路（Feed-forward Neural Network），吃的是每個 字 一個 向量。這時候就是要再乘上 將這一大串的矩陣再轉回成一個字一個向量（因為在圖中是兩個字，所以會變成是兩個矩陣）。

那我們綜觀下來，self-attention 的機制就如下圖運作。

Multi-head Self-attention Mechanism 哪裡比較好？

1. Multi-head 的機制更可以讓模型專注在一句話中的不同字上。雖然說在 Single-head 的機制底下，對其中一個字來說，一句話的其他字在這個字的編碼中會含有一點點的權重，但在某些情況下，還是有可能會特別側重在某個字上。但 Multi-head 就可以淡化這個問題。

2. 若你還記得的話，Multi-head 的機制針對一句話中的不同字，各自會有不同的 https://chart.googleapis.com/chart?cht=tx&chl=W_%7Bi%5EQ%7D 、
   以及 權重，這麼一來也可以提供模型的語意空間更高的彈性。（這是我的理解，若有錯誤還請前輩不吝指正。）

位置編碼（Positional Encoding）

要知道字在文中的不同位置對於語意理解上也扮演著很重要的角色，所以我們必須在模型中加入位置的資訊，也就是所謂的位置編碼（Positional Encoding），這可以幫助模型理解一個字在資料中的位置，以及與其他字的距離。

實際上會長這樣：

殘差標準化（Residual & Normalization）

因為在運算資料的過程中會產生殘差，所以也要經過標準化。這層標準化層，在編碼器以及解碼器中都會加入。

解碼器（decoder）

在編碼器，我們將文本序列作為輸入資料，在最後一個編碼器會得到兩個 attention vector，分別是 以及 。 這兩個向量可以幫助在每個解碼器中的 encoder-decoder attention 了解輸入序列中這些字的資訊。

在接下來的解碼中，除了前面兩個 attention vector 的幫助，同樣也會在解碼器端加入前文的 word embedding 以及 positional encoding，同樣也是為了要幫助模型了解語意距離、位置資訊等等，以利模型進行解碼。

最終輸出層（Final Linear and Softmax Layer）

最後一哩路啦！在解碼器的尾端，我們最後得到的輸出是由浮點數所組成的向量，但我們需要文字輸出的話，該怎麼辦？所以最後就會需要線性層（Linear Layer）以及激勵函數層（Softmax Layer）來幫助模型將這些數值資料轉回文字。

線性層是一個完全連接的神經網路。簡單的說，線性層可以將解碼器的輸出向量轉化成另外一種可以「儲存字彙」的向量，文中稱為 Logits vector。假如說今天模型在訓練資料中學習了 10000 個字，那麼在這個叫 Logits vector 的向量中就會有 10000 個元素，這些元素分別又代表了不同分數（score），這些分數都可以對應回去每一個字。

Softmax 則會在這10000個元素中的每一個元素各分配一個概率，讓模型用這個概率決定該以哪個字作為最後的輸出。

問題與討論

1. 解釋力偏低：由於 Transformer 算是深度學習模型的其中一種，所以通常解釋力都比較低。我們沒有辦法跟人解釋模型是如何運算得出某個特定的輸出結果。其實無論是 Transformer 還是前面介紹的 RNN，還有接下來要介紹的 BERT，都有一樣的問題。
2. 難以控制自注意力機制的運作：因為自注意力的運算機制，導致模型有漏字的可能。舉例來說，我們透過Google翻譯 one one one one two two one one twenty two 可以得到 一一一二二一一二二 ，但我們都知道少了一個一。 Source
   
3. 訓練時間長：我們用了好多attention head、好多的參數、好多的運算，那訓練一個模型的時間就會拉的特別長。一天兩天已算少，一週兩週剛剛好。

結語

好！既然我們已經了解了什麼是 Transformer，就代表我們已經做好萬全準備進入現在最強最常用的語言模型 BERT 啦！我們明天見！

參考資料：

1. The Illustrated Transformer
2. 謦伊的閱讀筆記

如果我能看得更遠，那是因為站在巨人的肩膀上。
牛頓

經過了前幾天的旅程，相信大家對於運用在自然語言處理的神經網路，應該已經有了一定程度的認識。神經網路是深度學習的起點，我們一路從機器學習一直到現在的深度學習，其實都依循著一定的脈絡在往前走。不知道大家是否還記得我們在旅程一開始的時候曾經說過，為了要讓機器學習模型理解文字，首要工作是要將文字轉換成數字，因此發展出了許多如詞頻、TF-IDF等以詞為模型理解語言的最小單位的方式，接著以詞頻為基礎，將語言理解成具有統計概念的分布模型，因此這樣的模型被稱為語言模型，接著將這些轉成數值的文字資料放進傳統機器學習模型。後來，人工智慧學家發現，比起讓模型從詞彙的角度出發，讓模型可以理解文字、句子、甚至是文章上下文之間的連續關係，其實應用上可以更為廣泛。

就跟我們人有著不同專長一樣，不同的模型也擅長處理不同的資料。當模型處理具有序列關係的資料時，這種sequence model就是最好的選擇，也就是說，我們前幾天所說到的模型，RNN、LSTM、GRU等，都是sequence model的一種。

今天要介紹的，也是一種sequence model，稱為Transformer。今天這篇文將會有很大一部分是來自於 The Illustrated Transformer這篇文章，若各位想拜讀原文，可以毫不猶豫地點進去這篇文章喔！

自然語言處理的變形金剛：Transformer

如果我們將模型視作一個黑盒子，那首先要先釐清，輸入模型的資料型態會是一個句子，輸出也會是一個句子（畢竟是sequence model，輸入及輸出也會是 “sequence”），而在這個模型內部，是由一長串的編碼器（encoder）跟解碼器（decoder）所組成。我們可以參考以下示意圖：

在圖中我們可以看到，輸入及輸出之間是由一串的編碼器和解碼器所組成。雖然在原文中的圖也是用各六個編碼及解碼器，但事實上跟6這個數字一點關係都沒有。 畢竟不是每個人都是諫山創一樣對數字有執著

首先我們先來將注意力放在編碼器（Pun intended！），編碼器的構造又是由 自注意力機制（self-attention mechanism）以及一組前饋神經網路（feed-forward neural network） 所組成。另外在解碼器中，除了自注意力機制以及前饋神經網路之外，也多了編解碼注意力機制（encoder-decoder attention），前饋神經網路在我的 神經網路也會神機錯亂？不，只會精神錯亂…深度學習：前饋神經網路 這篇文章中已經提過，想必大家應該都很清楚了（吧？）（嗎？）所以今天會將主力放在解釋何謂自注意力機制。

自注意力機制（self-attention mechanism）

自注意力機制的要點在於，深度學習模型可以判斷句子中某個字與句中其他字的關聯性大小，比如說，句中某個字的指涉對象是同一句中的哪個字。這樣說或許有點抽象，什麼指涉，什麼關聯性的吊書袋幹嘛？其實若用原文的舉例來說的話：

1

"The animal didn't cross the street because it was too tired."

在這句話中，it的指涉對象就是animal，也就是說，整句話之中，it跟animal的關係最接近，所以模型在進行自注意力機制的時候，就會給animal比較高的權重。這個運作方式就像是先前在圓圓圈圈圓圓～深度學習：循環神經網路 RNN之中所說，RNN透過隱藏層之間的資料傳遞（也就是RNN的記憶能力）來了解當前處理的字，與先前處理過的字，兩者之間的關係。

如何計算的呢？

1. 步驟一：從編碼器輸入層中（在這裡則是詞嵌入層）中計算出三個向量，分別為key vector、query vector以及value vector。這三個向量分別乘上權重、 以及 之後，就可以得到這個字在句子中的投射（projection），也就是用比較短的向量來代表一個字在一個句子之中的「定位」（我的理解，若有錯請指出）。

2. 步驟二：在這裡要做的是，要計算對當位置輸入字詞來說，其他字的「重要程度」。作法則是將計算所得的key vector，與自己還有其他字詞的query vector相乘（也就是內積），即可獲得前述所謂「重要程度」的分數。

3. 步驟三：再來就是除以8，接著把他丟入softmax激勵函數。之所以除以8的原因只是因為這是64的平方根，也就是key vector維度的平方根，這可以幫助在梯度下降時穩定找到最佳解。我們在這裡最終會獲得[0, 1]之間的數字。

4. 步驟四：最後就是相乘再相加。
   • 相乘：將Softmax所得的數值，乘以value vector。這裡的作用是，將重要的字保留下來，並將不重要的字過濾掉。（因為不重要的字會乘上一個超小的數值，就可以把他的重要性降低了）。
   • 相加：將前面計算的數值相加，就可以得到在這個「位置」的自注意層輸出了。

是不是已經腦洞大開了呢！但這還只是single-head attention，在原論文 Attention Is All You Need中其實又再針對這個概念進行了改良 套句高中數學老師說的，是想逼死誰？ ，加入了multi-head attention，而這可以更準確地判斷句中不同位置的字的相對重要程度，不過我們明天再來詳細介紹是怎麼回事，還有後續的decoder的運作方式；另外，朋友們也可以想想看，為什麼在文中，我只要寫到「位置」，我都會特別加上引號。不過我們在這邊先休息一下，明天進入Transformer 下篇！

我們透過最具革新性且客製化的裝修結構，將兩片晶片合在一起。這種雙晶片的結構領先於現今業界的任何一種晶片。
Apple Event, March 8, 2022, Introduction to Apple M1 Ultra

不知道你是否記得，我們在圓圓圈圈圓圓～深度學習：循環神經網路 RNN、跟你我一樣選擇性記憶的神經網路？深度學習：長短期記憶 LSTM，以及每天成為更好的自己！神經網路也是！深度學習模型 GRU 等三篇文章中有提到，因為這兩種神經網路模型都是由前到後地對資料進行「學習」，且相對於簡單的機器學習模型，神經網路有記憶特性，因此可以考慮到上下文的關係（儘管不同種神經網路有其各自的缺陷）。然而，LSTM 同樣也繼承著循環神經網路的其中一個缺點，而 GRU 雖然運算速度比較快，但作為 RNN 的一員，也是在劫難逃，而這個缺點就是無法考慮「下上文」的關係。

什麼意思？

下上文的關係

想像一下，我們要理解一段文字中的某一個字時，不只需要了解這個字的上一個字，有時候也會需要知道這個字的下一個字是什麼，才能確定這個字所真正代表的意義。舉例來說，讓我們看看以下這張圖：

source: Bi-LSTM

在圖中，單從前面的said並沒有辦法確定Teddy是什麼意思，因為Teddy有可能是一個人名（美國前總統 Teddy Roosevelt），也有可能是一種玩具（泰迪熊），而要確認Teddy指的是什麼，就會需要Teddy後面的字。比如說在這裡的狀況，若後面是bear，那就是一種玩具；若後面是大寫名詞，那代表這裡的Teddy很有可能是人名。

不然就是，左到右 LSTM 今天所學到的句子是「魯夫出海時搭著」，而右到左 LSTM 所學的是「打倒了近海王者」，那麼對於一個模型來說，有了上下文的資訊，就能比較準確地預測在中間的字是什麼吧！而對於RNN體系的單向神經網路來說，以上這些任務的表現就比較差了。

也就是說，我們前三天所介紹的三種模型：RNN、LSTM、GRU，都沒有辦法有效地解決這個問題。這時機器學習學家就想

「那既然原來的LSTM是從左邊到右邊學習，那就再放另一條LSTM從右邊到左邊，就好啦！」

當然我把它變得超級白話啦！但真的原理就是這麼簡單。所謂的BiLSTM，就是把從左到右的LSTM，以及從右到左的LSTM合在一起，就這樣！不可能是什麼雙性戀的LSTM的吧，誰知道LSTM的自我認同是什麼呢？(X)

從圖中我們可以看到，每一個節點的輸出，都是左到右 LSTM 跟右到左 LSTM 所綜合的結果，這就是我們前面所說，單純將兩個方向的 LSTM 結合，其實就可以很有效地解決RNN體系無法理解「下上文」的缺陷。

問題與討論

所以 BiLSTM 通常也可以有效地解決各類的自然語言處理任務，像是文本分類、機器翻譯、實體辨識等等，除此之外，在聲音辨識中，BiLSTM也是可以佔有一席之地的喔！

不過熟悉我前面文章風格的都知道，接下來就要講不好的地方啦！俗話說：「有一好，沒兩好。」記得前面在講LSTM的時候，有提到因為在節點中加入了三個門閥（輸入閥、遺忘閥、輸出閥），所以不管是訓練時間還是運算資源，消耗量都相當可觀。那聰明的你可以想想看，兩條 LSTM 會怎麼樣呢？

沒錯，BiLSTM是個運算量更大、訓練時間更久的深度學習模型！你可能會想說，有LSTM就有BiLSTM，那有GRU，就會有BiGRU吧？是有BiGRU的，但通常大家都會直接轉向我們自然語言處理界的超大型巨人 BERT 了。也就是說，從明天開始，會花三篇的篇幅來，從注意機制（attention）開始，一路到transformer，接著到BERT的介紹，之後才會進入實作，還請大家一定要撐下去啊（其實是在對自己說）！

若大家沒事的話，也可以點進昨天的文章，不知道為什麼點閱率少得可憐啊！

➡️ 【NLP】Day 17: 每天成為更好的自己！神經網路也是！深度學習模型 GRU
➡️ 【NLP】Day 16: 跟你我一樣選擇性記憶的神經網路？深度學習：長短期記憶 LSTM
➡️ 【NLP】Day 15: 圓圓圈圈圓圓～深度學習：循環神經網路 RNN

今天沒有引言，但是有梗圖

前天的文章介紹了基本的循環神經網路RNN，但RNN的致命缺點是容易導致梯度下降或是梯度爆炸。為了要解決這個問題，必須在以下兩點有所突破：

1. 優化梯度演算法
2. 在神經網路的節點中，設計較好的激勵函數（activation function）

昨天的文章所介紹的長短期記憶神經網路模型選擇往第二點的方向突破，在神經網路節點中加入了輸入閥（input gate）、遺忘閥（forget gate）、以及輸出閥（output gate），這個做法可以有效地解決循環神經網路模型容易梯度下降或是梯度爆炸的缺點，但由於長短期記憶模型加入的參數過多，若透過大量的資料進行訓練，可能會導致模型運算量過大。那電腦科學家們為了降低運算成本以及減少佔用記憶體，同時又要維持相同的模型表現，於是就發明了GRU（Gate Recurrent Unit）。

GRU

GRU 也是循環神經網路 RNN 的另外一種變體，因此網路架構也跟 RNN 相差無幾，GRU 同樣有輸入層、隱藏層、以及輸出層，最大的差別只是在於其中的節點運算。

我們可以回想一下，在LSTM中，總共有三個門閥對資料進行「把關」，分別為輸入閥、遺忘閥，以及輸出閥；而在GRU中，同樣也有門閥，功能也是完全相同（皆為篩選記憶），只是三個變成了兩個，分別為重置閥（reset gate）以及更新閥，由於減少了門閥數量，因此運算量相對於LSTM來說，減輕了不少。

GRU的內部結構

跟LSTM相同，我們先從GRU的兩個門閥開始，圖中的 是重置閥， 則為更新閥，兩者在各自的權重 乘上輸入 以及隱藏層 後，皆會經過激勵函數將數值變換成0-1之間的數字，篩選模型記憶的資訊，也就是說，這些數值代表節點對資訊的記憶程度。我們在這裡將 跟 計算出來之後，先放著備用。

接下來讓我們進入節點的設計，前面有說到 GRU 從原本 LSTM 的三個門閥變成兩個門閥，所以以下會分成兩個階段來講解。

重置閥

話不多說，先上圖！⊙ 代表矩陣相乘，⊕ 代表矩陣相加

請允許我把這部分用不到的路徑先遮蓋起來，這樣比較不容易迷路。

在這裡，我們會用到之前所計算的重置閥 （reset gate）。首先，當我們得到了重置閥r之後，要透過重置閥來「重置」上一個隱藏層傳來的資訊：

接著 與輸入 以及權重相乘後，再加入 的激勵函數，將資料壓到 [-1, 1] 之間，就會得到 。

• 代表意義： 主要是透過 來篩選上一層隱藏層 所傳來的資訊，接著結合本節點的輸入 。以上動作都是為了將 加入到這個節點的隱藏狀態。功能類似於LSTM的選擇記憶階段。

更新閥

透過這個更新閥，就可以同時做到記憶以及遺忘的功能。在這裡，我們會用到之前所計算的更新閥 （update gate），在這裡的計算是：

其中更新閥的數值，因為sigmoid激勵函數的緣故，數值會介在[0, 1]之間，這代表GRU在這一層需要記憶的程度。越接近1代表記憶的資訊越多；越接近0代表遺忘的資訊越多。 不知你是否發現到，只要單單透過一個門閥，就可以同時控制遺忘以及選擇記憶，相對於LSTM要用多個門閥才能達到相同的效果，這就是為什麼GRU的計算成本可以低於LSTM的原因。

• 代表意義：
  • 「忘記」上一層隱藏狀態所帶來的資訊比例，主要是要放掉上一層隱藏層帶來的不重要資訊，功能接近於LSTM的遺忘閥（forget gate）。
    
  • 表示從 中所要選擇記憶的比例。
    
  • 兩者結合起來就是忘記上一層隱藏層 所傳下來的資訊，並從當節點所接收的輸入資料中進行選擇性記憶。
    

問題與討論

因為GRU用了比較少門閥的緣故，所以相對於長短期記憶LSTM來說，訓練的時間較短，佔用的記憶體也較少。只是模型表現上，兩者其實是差不多的。所以如果考量到訓練時間還有運算資源的限制的話，鐵定是毫不猶豫地選擇GRU的啦！

不過就像在Day 15: 圓圓圈圈圓圓～深度學習：循環神經網路 RNN中所說，這仍然無法解決模型無法理解下文與上文之間關係的問題。那人工智慧學家又是怎麼解決這個問題的呢？就讓我們等到明天介紹BiLSTM的文章再來聊吧！

若你有空，也歡迎來看看其他文章：

➡️ 【NLP】Day 16: 跟你我一樣選擇性記憶的神經網路？深度學習：長短期記憶 LSTM
➡️ 【NLP】Day 15: 圓圓圈圈圓圓～深度學習：循環神經網路 RNN
➡️ 【NLP】Day 14: 神經網路也會神機錯亂？不，只會精神錯亂…深度學習：前饋神經網路

記憶是個很奇妙的東西。他並不如我想像中那樣運作的。我們太受限於時間了，尤其是時間的順序…
《異星入境》Louise Banks

昨天我們剛介紹完循環神經網路（Recurrent Neural Network），提到說雖然循環神經網路很常被拿來利用在自然語言處理上，原因是因為循環神經網路有記憶的功能，可以考慮到輸入文本的上下文關係，並藉此來達到更好的效果。

但再厲害的技術，也都會有它優缺點，就如同我第一週所說的那樣，科學的演進都源自於對完美的追求，這也正是 Steven Pinker 在《再啟蒙的年代》一書中所說，只要是可以衡量的事物，而這些事物若是有所變化的，那就是人類社會便是一直在進步的路上邁進。

所以說同樣地，RNN 也有先天上的缺陷。像是因為過多層神經網路導致的梯度爆炸或是梯度消失，影響了模型學習成果以及表現，最後的準確度反倒下降了。昨天說到，LSTM 就是 RNN 的是日救星。

長短期記憶模型（Long Short-term memory）

這邊用一個簡單的例子再來重新解釋梯度爆炸跟梯度消失：假如說我們今天利用以下的資料訓練一個可以完成QA任務的循環神經網路。

1

魯夫說他想成為海賊王

在最後測試模型時，問了模型：「是誰想要成為海賊王？」。這時候可能會出現一個問題：

記不記得我們先前所說 RNN 的記憶特性，而會有這個特性正是因為模型也會將先前所學習的詞彙資訊（權重）在隱藏層中傳遞，最後才會得到的結果。之後，模型會將這個結果進行反向傳播，也就是模型在「反省」先前的學習成果時，都會乘上一個自己的參數 ，若這個參數 的話，在資訊通過不同節點的過程中，若太多層神經網路，則會越乘越小，最後無限逼近於0，模型也就「忘記」先前所學的資訊，是為梯度消失；反之，若，某個資訊的概率也就越乘越大，而神經網路就被撐死了，是為梯度爆炸。

由於「是誰想要成為海賊王？」的答案（魯夫）在訓練資料中幾乎是在最前面的位置。若模型產生梯度消失的現象，答案在訓練的過程中就會漸漸地被模型「忘記」，最後模型就無法正確回答問題的答案，準確率就下降了。而長短期記憶就可以有效解決這個問題。

到底什麼是LSTM？

LSTM（Long Short-term memory），作為循環神經網路的一個變體，可以先從這張圖來理解，在這邊允許我借用左岸朋友莫煩大大的劇情比喻。

我們可以這麼理解，首先將藍色粗線視為電影的主線劇情、紅色線是為支線劇情，而輸入、忘記、以及輸出都是劇情的「把關者」。今天，「輸入把關者」在看電影時，會決定支線的劇情有多少對電影結局有影響，並依照劇情重要程度寫入主線劇情；但假如這些分線劇情會改變我們對於先前主線劇情的看法的話，「忘記把關者」就會將之前的主線劇情忘記，按照比例替換成現在的新劇情。也就是說，主線劇情的組成主要取決於「輸入把關者」跟「忘記把關者」。也就是說，相對於什麼都記，但時間一久就會忘記的單純循環神經網路，LSTM 則是會「選擇重點記，而且記得比較久」。

熟悉概念後，我們來看看數學原理以及模型吧！

這是台大李弘毅教授機器學習課程中的投影片。在圖中，我們可以看到左邊的是一般的循環神經網路，右邊的則是 LSTM。可以發現，兩者最大的差別就是，LSTM 多了一個變數 ，稱為cell state，也就是前面所說的支線劇情。 改變速度很慢且幅度小，而 的改變速度則較快，而且幅度比較大。

在進入一個新節點時，總共得到四個狀態，分別是, , , 。 作為主要的資料輸入，而另外由激勵函數所包起來的 , , ，則是作為前面所說把關的三個「門閥」。

而這四個狀態分別在長短期記憶的一個節點中，分別在運算的三個階段中扮演著不一樣的角色。先讓我們來看看以下這張圖，其中⊙代表矩陣相乘，⊕代表矩陣相加。（高中數學，還記得吧！）：

在這張圖中的運算過程共分成三個階段：

1. 忘記階段
   在這個階段會選擇性忘記上一個節點所傳來的資訊，簡單來說，就是決定「把重要的記起來，把不重要的忘記」。實際上的運算是，作為遺忘閥（forget gate），像篩子一樣，來控制上一個階段的哪些需要記得，哪些需要忘記。
2. 選擇記憶階段
   而在這個階段，LSTM 則會決定哪些是重要的資訊，而哪些不是，並將重點記起來。主要是透過輸入閥（input gate） 來決定當前的輸入內容哪些是重點，哪些不是。

   以上兩者所得結果相加，就會是這個階段的。

3. 輸出階段
   這個階段則是以前述兩者之和，經由激勵函數的縮放後，以來決定經過的 資訊中，有哪些適合做為當節點的輸出，並計算出下一個節點的 。

問題與討論

在過去讀書階段中，各位一定都有碰過兩種同學，一種是死命地想辦法將所有資訊記下來的同學，另一種則是只記重點，一些太枝微末節的小細節就會選擇性地放棄。而因為前者想要將所有東西都記下來，看起來好像很厲害，但時間一久反而會忘記最重要的重點，考試的表現就容易比較差，這種的大家通常都會說「沒有讀書方法」；反而是後者因為只記重點，所以記的東西就比較少，反而不容易忘記，考試的表現就會比前者還要好。

所以說，拉回來神經網路，比起 RNN 那樣死命地將所有的資訊記起來，不僅容易忘記先前所記下來的資訊，最後的表現也不會好；相對的 LSTM 會忘記不重要的資訊，只記得重要的，表現結果就會比較好。

需要改進的地方

1. 語意限制：同樣是RNN的一種，所以也遺傳了RNN的其中一個缺點，詳見：Day 15: 圓圓圈圈圓圓～深度學習：循環神經網路 RNN
2. 訓練複雜度提升
   相對於 RNN，我們光是看圖就可以發現，LSTM 其中新增了許多的參數，那一旦資料量提升，訓練複雜度也就會增加。而為了解決這個問題，資訊科學家又發明了與LSTM相同效果，訓練又較不複雜的 GRU（Gate Recurrent Unit），來搭建資料量大的模型，也就是我們明天的文章內容。

下一篇文章

➡️ 【NLP】Day 17: 每天成為更好的自己！神經網路也是！深度學習模型 GRU

若你有空，也歡迎來看看其他文章

➡️ 【NLP】Day 15: 圓圓圈圈圓圓～深度學習：循環神經網路 RNN
➡️ 【NLP】Day 14: 神經網路也會神機錯亂？不，只會精神錯亂…深度學習：前饋神經網路
➡️ 【NLP】Day 13: 可不可以再深一點點就好？深度學習基礎知識：你需要知道的這些那些

對啊，這也是一種世界。也是我心中的可能性。現在的我並不只是我，還可以有很多種自我。
《新世紀福音戰士》碇真嗣

循環神經網路（Recurrent Neural Network），作為神經網路的其中一種變體，是在所有神經網路的模型中，最常被拿來應用在自然語言處理任務的模型之一。原因有二，首先，相對於其他的神經網路模型，循環神經網路模型的輸入資料較為彈性，意即當其他的神經網路只能接受固定的字數時，循環神經網路亦能透過不同長度的文本輸入進行訓練；二，語言中我們常說要了解上下文、語境，才能對語言有更完善的判斷，而循環神經網路的記憶功能就可以做到考慮文本上下文的效果。因為以上兩種原因，循環神經網路才會是所有神經網路中最常應用在自然語言處理上的深度學習模型。讓我們一起來看看為什麼吧！

基本結構

在正式進入架構之前，要先將循環神經網路跟其他神經網路進行區別。跟先前所介紹的神經網路模型相同，一個完整的循環神經網路模型同樣也有輸入層、隱藏層，以及輸出層，但既然基本架構都相同，那最關鍵的差異點在哪裡呢？我們先來觀察以下這兩張圖。上圖是人工神經網路，是輸入， 是輸出；下圖則是循環神經網路， 是輸入， 則是輸出，其中是隱藏層。

Credit: Speech and Language Processing

Credit: kdnuggets.com

不知道大家有沒有發現到，這兩張圖之中最大的差異就在於，循環神經網路的隱藏層會自我循環，也就是說，若將隱藏層拆開來看的話，隱藏層中的節點會接收上一個隱藏層節點所傳過來的權重。也就是說，對資料的每一個節點來說，就像是碇真嗣所說：「現在的我並不只是我，同時也包含了過去到現在的很多種自我。」所以我們重新回來看神經網路的圖示架構可以發現，正是因為這樣的特性，循環神經網路才有記憶的功能。

理解循環神經網路最大的特色之後，再讓我們回來看其中的數學運算原理。其實除了隱藏層之間的連接特性之外，循環神經網路的計算也跟一般的神經網路大同小異。首先是輸入資料與權重相乘，接著再跟上一個隱藏層神經元所學習到的資訊與權重相乘，再把兩者相加，把相加之後的值加入激勵函數，稱為當下隱藏層的輸出，接著當下的輸出層即是隱藏層輸出乘上另一個權重，再經由激勵函數產生輸出。

應用

除此之外，循環神經網路彈性的輸入與輸出特性，也讓我們在各種下游任務間來去自如，其輸入與輸出及對應的功能如下：

1. 一對一（one to one）：輸入（input）及輸出（output）皆為固定，例如文本分類時輸出機率等。
2. 一對多（one to many）：單一的輸入，但是可以有複數個輸出，例如文本生成，給予一個主題，使模型透過這個主題生成一串文本。
3. 多對一（many to one）：多個輸入，但只有單一輸出，例如情感分析(Sentiment Analysis)，我們可以輸入任一一段文字，並使模型判斷這段文字正面以及負面情緒的程度。
4. 多對多（many to many）：複數個輸入，複數個輸出，例如機器翻譯(Machine Translation)，輸入一段外國語言的句子，模型將這段話翻譯成中文。

問題與限制

• 語意限制
  前面提過，循環神經網路有記憶的特性，因此可以將上下文也考慮進去。但其實嚴格來說，如你們在圖中所見，隱藏層中的節點只能接收上一個隱藏層的節點，沒有辦法同時也接收下一個隱藏層節點的資訊。聽起來很抽象，但這其實就意味著模型雖然可以記住上文，並消化下文，但卻也因為這個特性，使得模型無法理解下文與上文之間的關係。
• 梯度消失
  當神經網路在反向傳播中，也就是模型向回修正，並透過梯度下降法在找尋最佳解，找Loss的最小值時，可能會發生一個現象，就是梯度會越來越小、越來越小，最後變為零。這就導致模型沒有辦法再繼續找到最小的Loss。
• 梯度爆炸
  梯度爆炸正好與梯度消失相反，梯度會越來越大、越來越大，導致越接近淺層網路，權重變化就越大，也會造成模型訓練上的反效果。

那該如何解決梯度消失以及梯度爆炸的問題呢？其實一般來說，在自然語言處理的任務中，不會僅僅只用循環神經網路，也會在裡面再加上另外一層深度學習模型：長短期記憶（LSTM）。同時應用循環神經網路以及長短期記憶模型，就可以有效避免梯度消失以及爆炸的問題了。

那我們明天就相約在長短期記憶見囉！

下一篇文章

➡️ 【NLP】Day 16: 跟你我一樣選擇性記憶的神經網路？深度學習：長短期記憶 LSTM

若你有空，也歡迎來看看其他文章

➡️ 【NLP】Day 14: 神經網路也會神機錯亂？不，只會精神錯亂…深度學習：前饋神經網路
➡️ 【NLP】Day 13: 可不可以再深一點點就好？深度學習基礎知識：你需要知道的這些那些
➡️ 【NLP】Day 12: 豬耳朵餅乾跟機器學習也有關係？機器學習：羅吉斯回歸

在夜城，不要相信任何人，受到背叛也是自己的錯…
琦薇《電馭叛客：邊緣行者》

我很喜歡賽博龐克風格的相關作品，像是銀翼殺手、攻殼機動隊，都是我很愛的作品。最近在看《電馭叛客：邊緣行者》（好看，推薦大家去看），在動畫中，或是說在賽博龐克風格作品中的人物，為了要達到更高更強大的身體能力，會用電子零件（像是電子手臂，或是增快移動速度的軍事武器植入物等）將身體的一部分改造。而在電馭叛客中有個名詞：神機錯亂，意指若身上已經乘載過多改裝與植入，這些電子組件會侵蝕人性，並擾亂心智，到最後迷失自我。

最近在寫神經網路的我，突然覺得神經網路跟神機錯亂真像。在一開始，疊了一層兩層的神經網路，得到了還算可以（夠用）的結果，但為了要達到更高的準確度、更好的表現，疊了更多層的神經網路上去，卻在梯度下降找最佳解時，碰到梯度爆炸或是梯度消失的問題，最後就一直徘徊在局部最小值的谷底出不來，然後他就停止學習了，不就很像神機錯亂嗎？

扯遠了不可能每次都扯遠吧，今天首先要介紹的是前饋神經網路，若說機器學習的第一個模型是貝氏分類模型，那麼深度學習就一定要從前饋神經網路開始講起。首先會先從神經網路的基本結構開始，一直到自然語言處理實務上的操作，話不多說，就讓我們開始吧！

神經網路的結構

神經網路的基本架構大致上可以分成三個部分：

• 輸入層（input layer）：初步資料會先經過輸入層進行處理。在自然語言處理中通常會是傳遞給embedding layer的one-hot vector。
• 隱藏層（hidden layer）：隱藏層可以有一層以上，在隱藏層中，會透過「權重」計算輸出。通常隱藏層會篩選出多餘的資訊，並將所習得之重要資訊傳遞給下一層隱藏層。
• 輸出層（output layer）：學習成果，通常會是以機率的形式呈現。

神經元

這些神經層中，是由一個一個的節點組成，這些節點有時候也會被稱為 「神經元」（neuron） ，這些節點其實就是將特徵乘上權重，再加上一個偏項b，那麼很多個節點所組成的神經網路，事實上也就是很多個函式所組成的函式組！

有沒有覺得很熟悉，因為這個計算方式跟羅吉斯迴歸一模模一樣樣！！！ 也就是當時在羅吉斯迴歸時所說的計算原始分數，再將我們計算的z值，也就是原始分數，放入激勵函數，將線性解轉換成非線性解，因為有些狀況之下，線性解並無法解決。

比如說像以上這種狀況，要畫一條線把藍點跟白點分開，左邊數過來第一張圖跟第二張圖都可以只利用一條線將兩者區別，但難保現實中會有第三張圖，這時候就會需要非線性解來幫助我們解決這種類型的問題。

激勵函數

我們在前幾天有討論過Sigmoid以及Softmax，這裡就先不贅述，若遺漏掉那部份的可以回去看我之前的文章。今天要來討論另外兩個激勵函數，也就是tanh 以及Rectified Linear Unit（ReLU）。

A圖是tanh，B圖是ReLU，一樣也是各有優缺點。

• tanh函式：在接近上下界時也趨近於平，所以也能像Sigmoid一樣擅長處理離群值，另外一樣也可以微分，記得先前所說找最佳解時，可不可微是很重要的特性，通常我們希望可微啦，人稱欲可微。
• ReLU：結果可以非常接近線性。

但像是Sigmoid或是tanh這種上下界趨平的函式，一階導數很有可能接近於零，接近零的結果，就是在進行梯度下降時發現梯度不見，模型也停止學習了，這就是所謂的梯度消失（gradient vanishing）

梯度下降

詳見我先前的文章：【NLP】Day 12: 豬耳朵餅乾跟機器學習也有關係？機器學習：羅吉斯回歸

Error backpropagation

神經網路有另外一個優點是，如果發現錯誤，模型會往回修正。但這部分有點複雜，我們在之後的文章再詳細介紹。

自然語言處理的運作

自然語言處理上的神經網路又有一點不一樣，在這裡為了處理訓練資料中所沒有的資料，會再多一個嵌入層（embedding layer）。

1. 輸入層（input layer）：one-hot vector
   自然語言處理的第一層神經網路通常會是one-hot vector，通常是為了標注其在嵌入層中的位置，藉此幫助模型更好理解語意。假如說今天海賊王在embedding layer中的第三個位置，並假設embedding layer的矩陣維度為5，那麼one-hot vector就會是[0, 0, 1, 0, 0]。
2. 嵌入層（embedding layer）
   記得在講Word2Vec時（忘記的話可以回去複習 Day 9: 又是國王皇后的例子啦！Word2Vec、N-Gram，我這篇的點閱率低的可憐。）我們有提到可以訓練一個word embedding，讓電腦了解語意間的關係，但是要注意這裡的語意關係很吃訓練資料的領域跟品質。這麼一來，即使出現了模型先前沒「看」過的字，透過這個embedding也能較好地處理這類的問題。比如說：

   1 2	training data: 索隆/跟/龍馬/拿/劍/決鬥 test data: 鷹眼/跟/比斯塔/用/劍/對決

   即使模型沒有在訓練資料看過鷹眼，但是因為Word embedding，我們可以推斷「索隆」跟「鷹眼」有很近的「語意關係」（可能因為都是劍客？），所以還是能推斷「鷹眼」後面可能會出現的字，跟「索隆」很接近。
3. 隱藏層（hidden layer）
   再次乘上學習過後的權重。
4. 輸出層（output layer）：activation function
   同樣就是透過激勵函數輸出成機率，詳見前文。

就是這樣，明天見！

下一篇文章

➡️ 【NLP】Day 15: 跟你我一樣選擇性記憶的神經網路？深度學習：長短期記憶 LSTM

若你有空，也歡迎來看看其他文章

➡️ 【NLP】Day 13: 可不可以再深一點點就好？深度學習基礎知識：你需要知道的這些那些
➡️ 【NLP】Day 12: 豬耳朵餅乾跟機器學習也有關係？機器學習：羅吉斯回歸
➡️ 【NLP】Day 11: 什麼？妳男友有乾妹妹？那你很大機率被綠了！機器學習：貝氏分類器

人類與動物的學習大都是非監督學習。所以說如果「智慧」是一塊蛋糕，那麼非監督學習才是蛋糕本體，監督學習則是那層糖霜，強化學習不過是上頭的櫻桃。
Most of human and animal learning is unsupervised learning. If intelligence was a cake, unsupervised learning would be the cake, supervised learning would be the icing on the cake, and reinforcement learning would be the cherry on the cake.
楊立昆 Yann LeCun

不知道昨天大家有沒有看到一則偏宅的新聞，就是星際大戰中達斯維達的配音員詹姆士・厄爾・瓊斯（James Earl Jones），從今開始正式不再為達斯維達配音。我們再也沒有機會聽到本人講那經典的台詞：

喔，對了，防雷警報，達斯維達其實是路克・天行者的老爸。（誰在乎？）

但是新聞還說，雖然本人不再配音，我們在電影中仍然還是可以聽得到他那經典的呼氣聲，並感受它強大的原力？為什麼？這一切都拜那個離我們又遙遠又接近的深度學習技術所賜。

其實不僅僅是語音合成，文本處理上現在也很流行利用深度學習的技術來完成任務。今天，就讓我們先來簡單大概了解什麼是深度學習，還有大家在吵什麼。

釐清名詞觀念

在開始之前，我們得要先釐清名詞觀念。從以前到現在，我們已經學到了好多名詞：人工智慧、機器學習、深度學習、監督式學習、非監督式學習，那這些名詞之間到底有什麼不一樣呢？我們可以這樣理解：

Source: NVIDIA

人工智慧是一個「雨傘術語」（umbrella term），而機器學習則是人工智慧底下最廣為人知的一個分支。主要目的在於設計和分析一些讓電腦可以自動「學習」的演算法，並利用規律對未知資料進行預測。機器學習又是另外一個「雨傘術語」，因為機器學習又根據演算法分為很多種不同的學習方法，我們這邊提到了監督式學習跟非監督式學習，如果沒看過我之前針對兩者差別進行的介紹，可以去看這篇 **Day 10: 進入偉大航道！機器學習基礎知識：你需要知道的這些那些**。而深度學習是機器學習的其中一種方式。

什麼是深度學習？

深度學習作為機器學習的其中一個分支，若要「沒那麼精確」但要淺顯易懂的解釋，你可以將深度學習理解成「比較深的神經網路」目的在於將資料放進多個節點，經過線性以及非線性的轉換，從原始資料中自動抽取足以代表資料的特徵，自動抽取特徵這點又被稱為表徵學習（representation learning），最終都可以得到非常優秀的結果。

類神經網路通常會有好幾層，每一層會有許多個節點（perceptron），就像人類的神經系統中，神經元與神經元之間的連結一樣，節點與節點之間也會彼此傳遞資訊，之後再經過激勵函數（activation function）轉換成輸出。

為什麼深度學習逐漸變成主流？

但其實深度學習的歷史已經非常悠久了。早在六七零年代，就有電腦科學家嘗試重現生物神經網路的架構，希望電腦可以達到跟人類一樣的優秀學習能力。但礙於當時電腦的運算能力還跟不上理論，再加上數位化的資料並不多，無法提供神經網路好的學習資源，所以當時神經網路仍無法展露頭角。

但現在拜於網路與資訊技術的進步，有越來越多的數位資料可以提供這些神經網路小試身手，除此之外，逐漸成熟的GPU演算技術也幫助了神經網路的運算，速度也有大幅成長（但仍然很慢），天時地利人和之下，神經網路這個名詞才漸漸重新浮出檯面。

跟前面提到的機器學習有什麼不一樣？

一般來說，像是我們先前所說的貝氏分類以及羅吉斯回歸這樣的監督式機器學習，都會需要我們手動加入特徵，而這些特徵都是透過我們人類觀察而得的；人工神經網路乃至於深度學習，其實並不需要我們人類進行特徵工程，深度學習模型會自己學習特徵並自動分類，最後輸出分類，但模型找的特徵可能跟我們一般所認知的特徵會有點差距就是了，也就是說，我們會看不懂神經網路找到的特徵。因此，人工神經網路也是黑盒子模型的一種，這部分後面我們會再提。

也就是說，資料越多，神經網路所能夠學的特徵就越多，深度學習模型的表現也就越好，好過過去監督式的機器學習模型。

可不可以再深一點點就好？越深越好？

深度學習的一個很常被討論的問題就是，既然叫深度學習，是不是越深就越好？現代知名電腦科學家楊立昆（Yann LeCun）在2008年的論文 Scaling Learning Algorithms towards AI 中就提到，在特定資料量底下，淺層架構的神經網路運算上或許沒辦法達到它最好的表現，深層才能達到最大效益。台大李宏毅老師在機器學習課程中也有提到，神經網路好像疊越多層、神經元越多，表現就越好。那我們就這樣一直無腦疊下去就好了嗎？模型就會越好嗎？

深度的特性反而是一把雙面刃？

後面我們會提到加深神經網路在優化上可能會發生的問題，比如像是神經網路的運算時間計算量大、耗時，即使是一個兩層三節點的神經網路，時間消耗仍然為NP-Complete，NP-Complete就是運行複雜程度的等級，詳細可以來看這篇前輩的文章。另外，也因為梯度消失以及梯度爆炸的現象（後面文章會介紹），也會導致神經網路找不到最佳解，你可以回想前面我們說羅吉斯迴歸為凸函數，找得到最小值；但神經網路為非凸函數，有可能只找到局部最小值，那該怎麼辦呢？

答案是，不怎麼辦！因為我們不能保證模型找到最佳解，但是找到的最小值已經非常逼近最佳解，也就是說已經夠好到足以幫助人類完成許多任務了！

所以其實還是老話一句，越深越好？還是要看任務是什麼，找到最適合的方法才是最重要的。

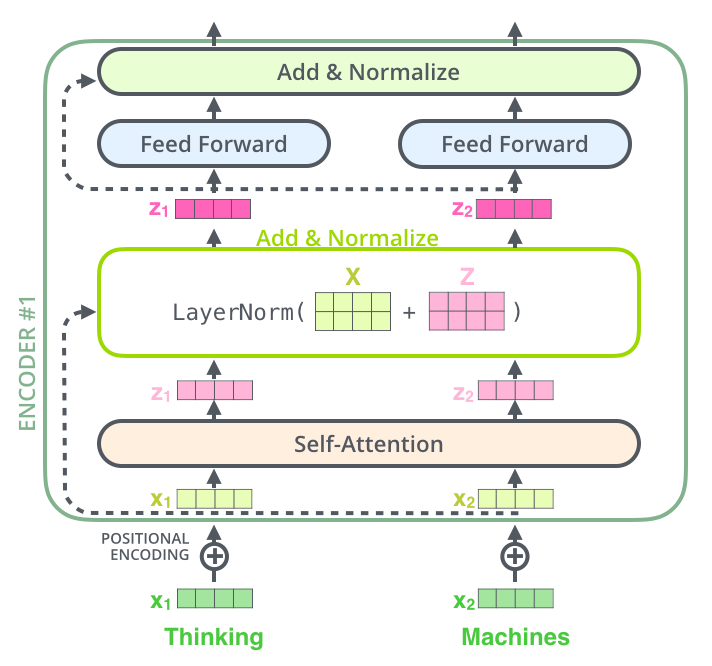
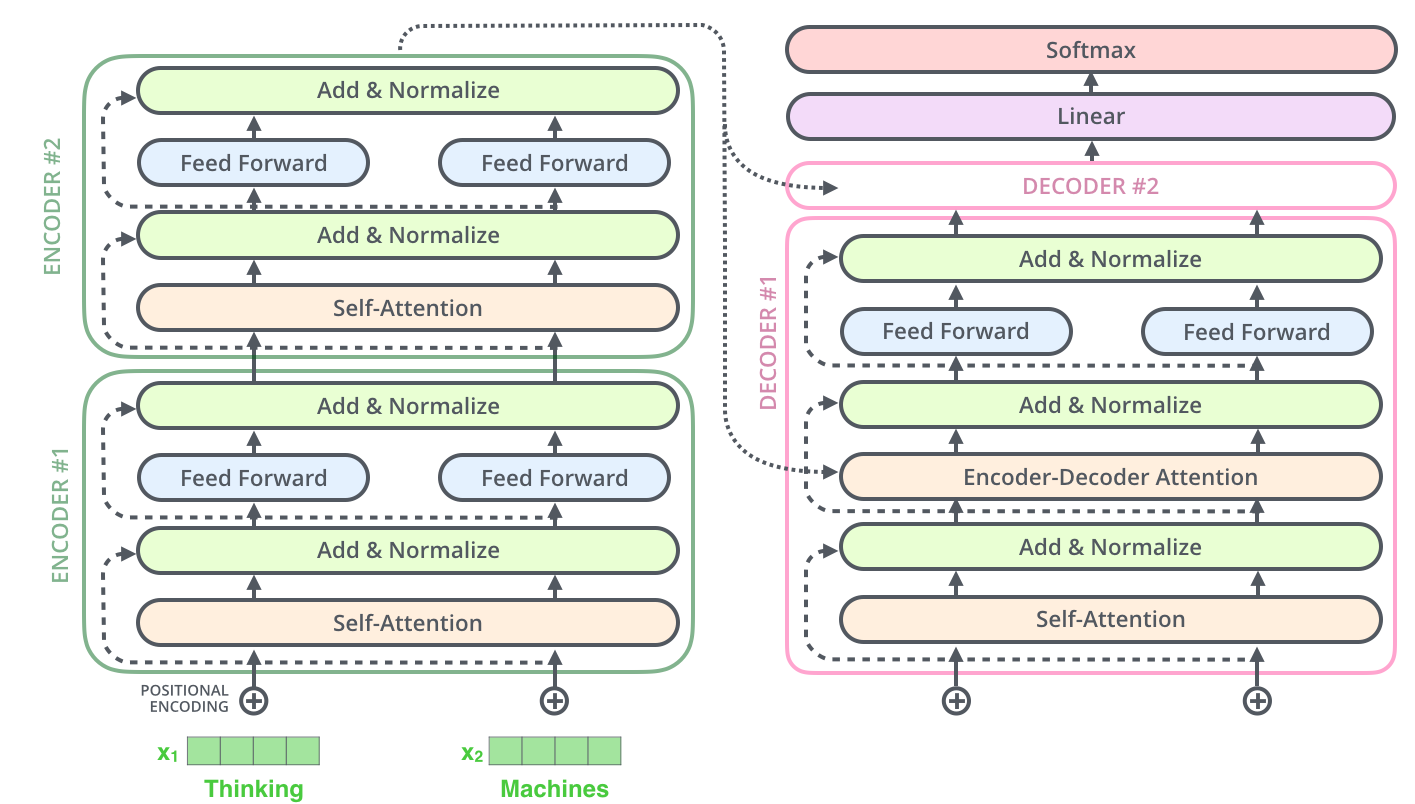
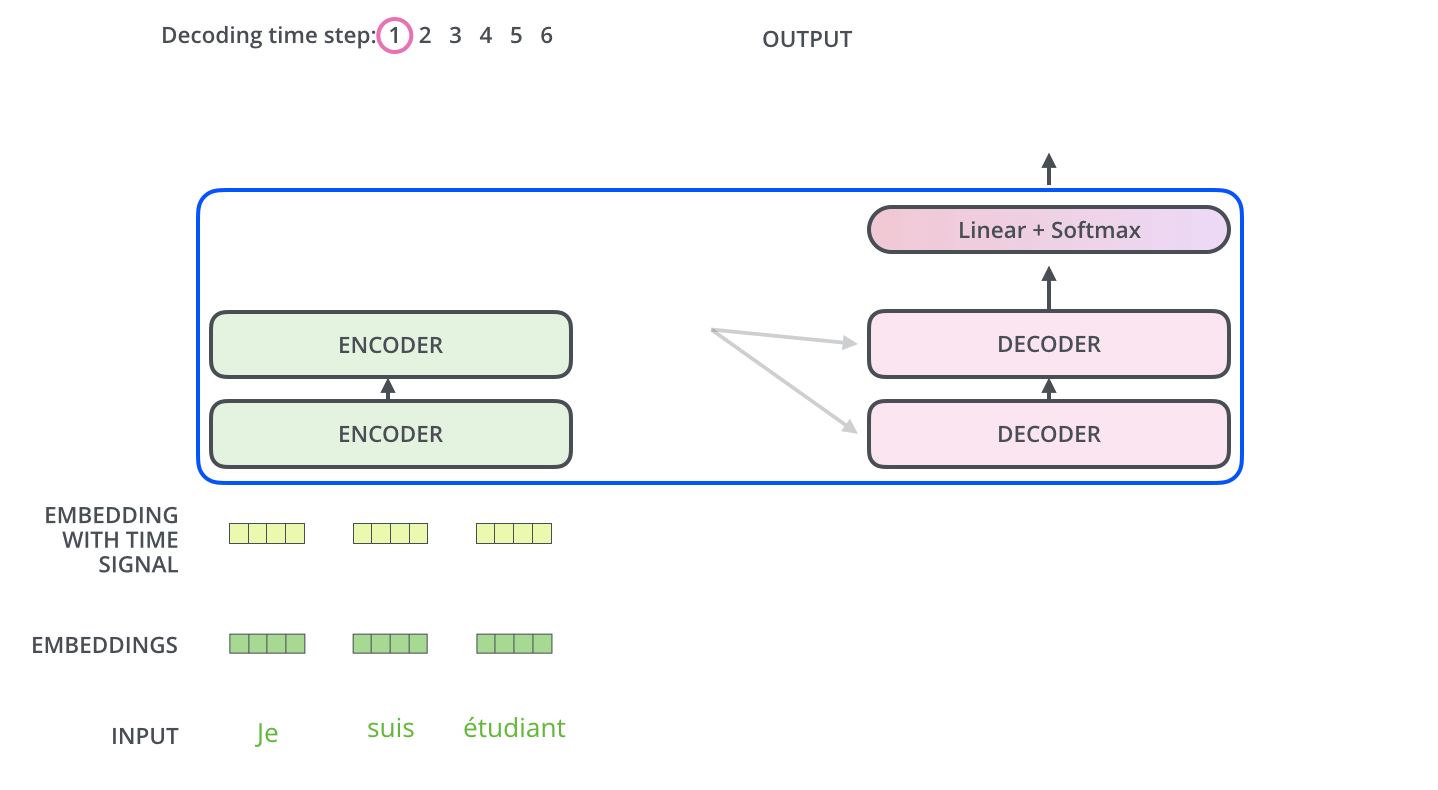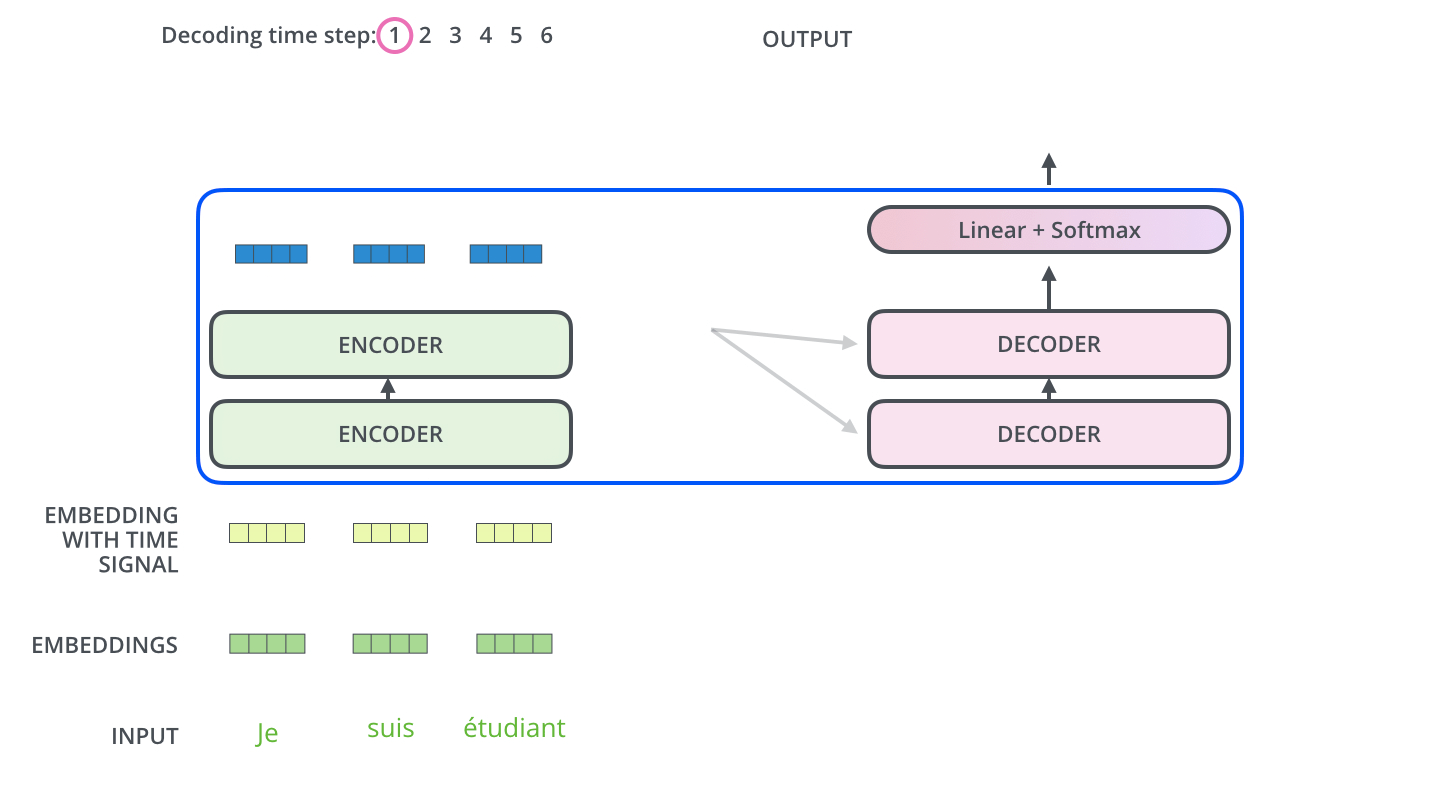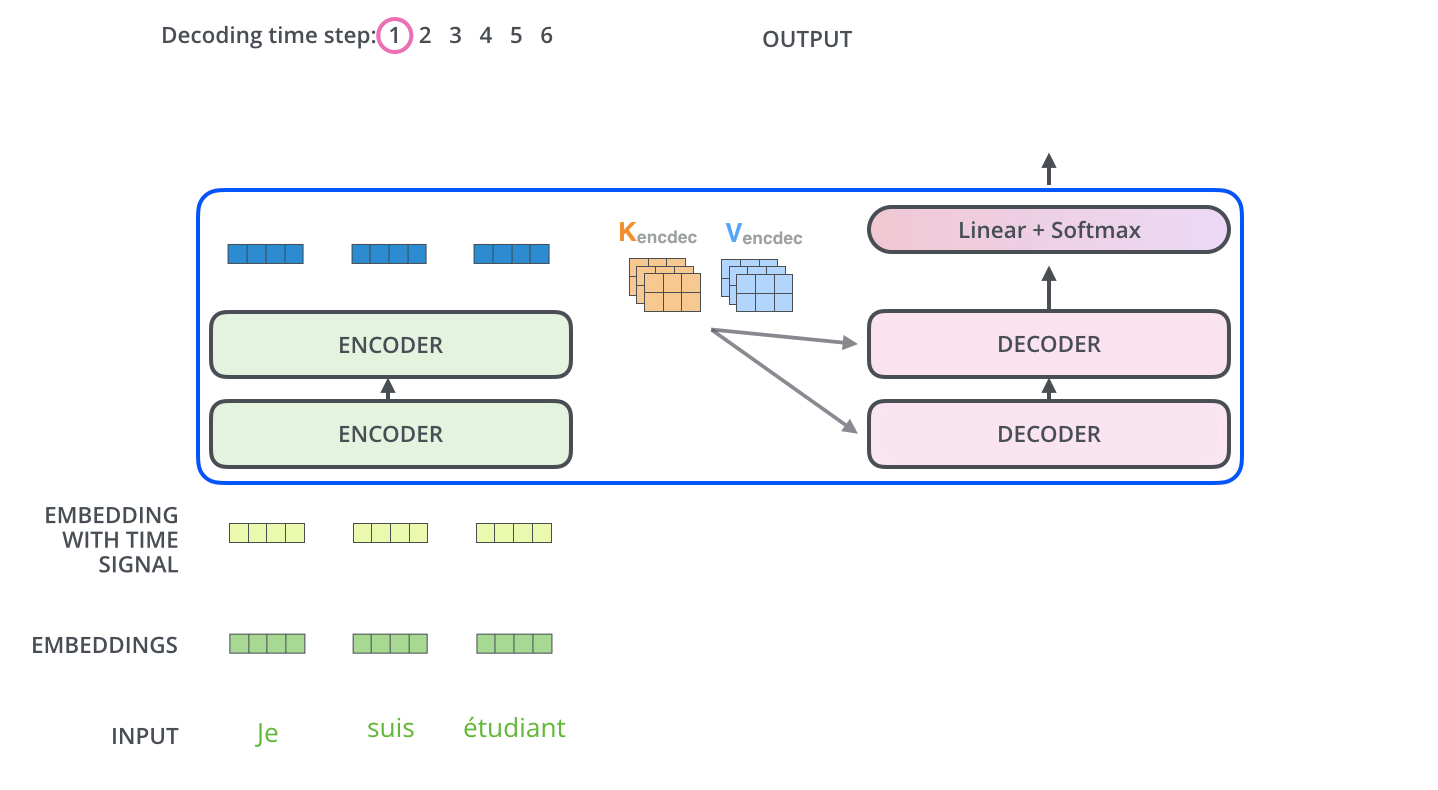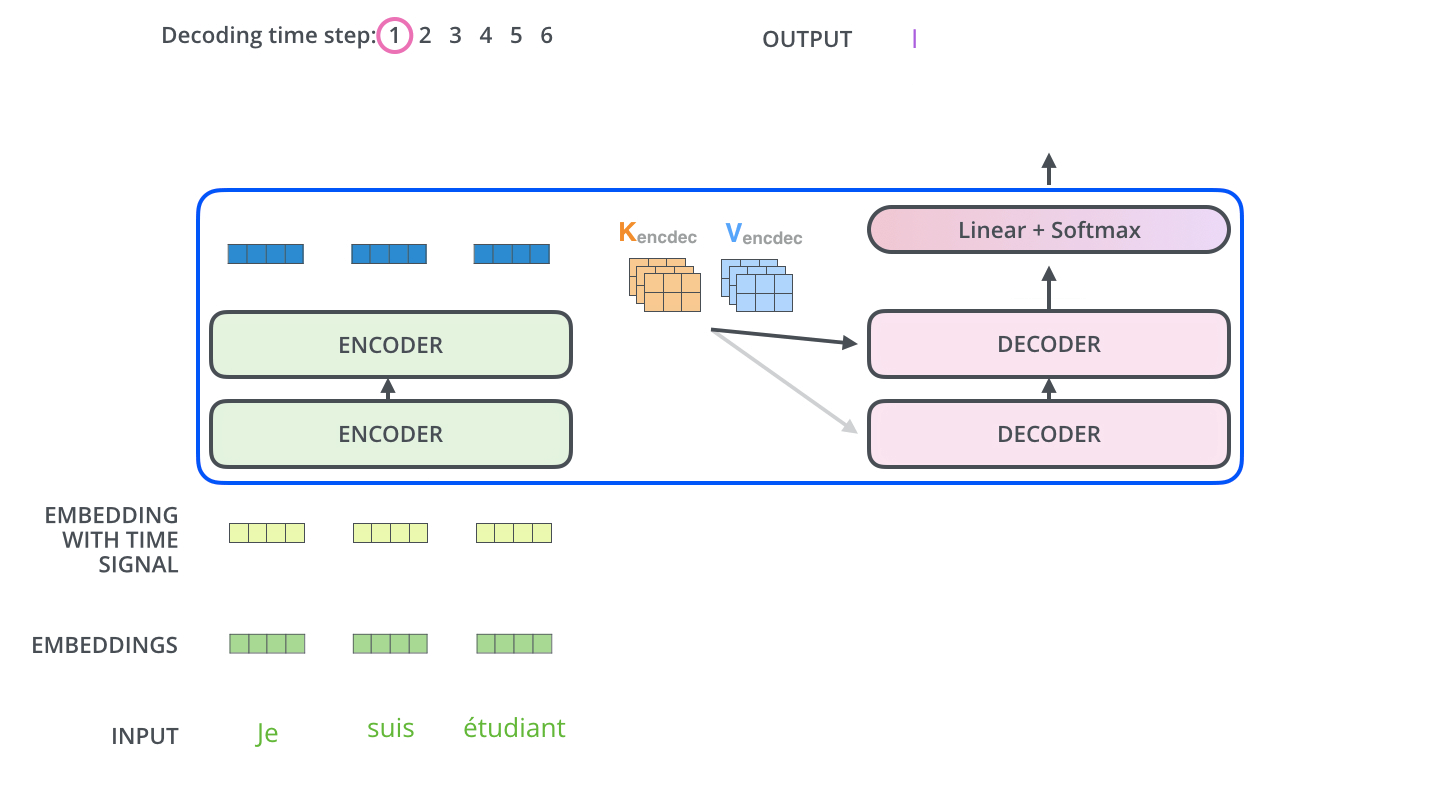
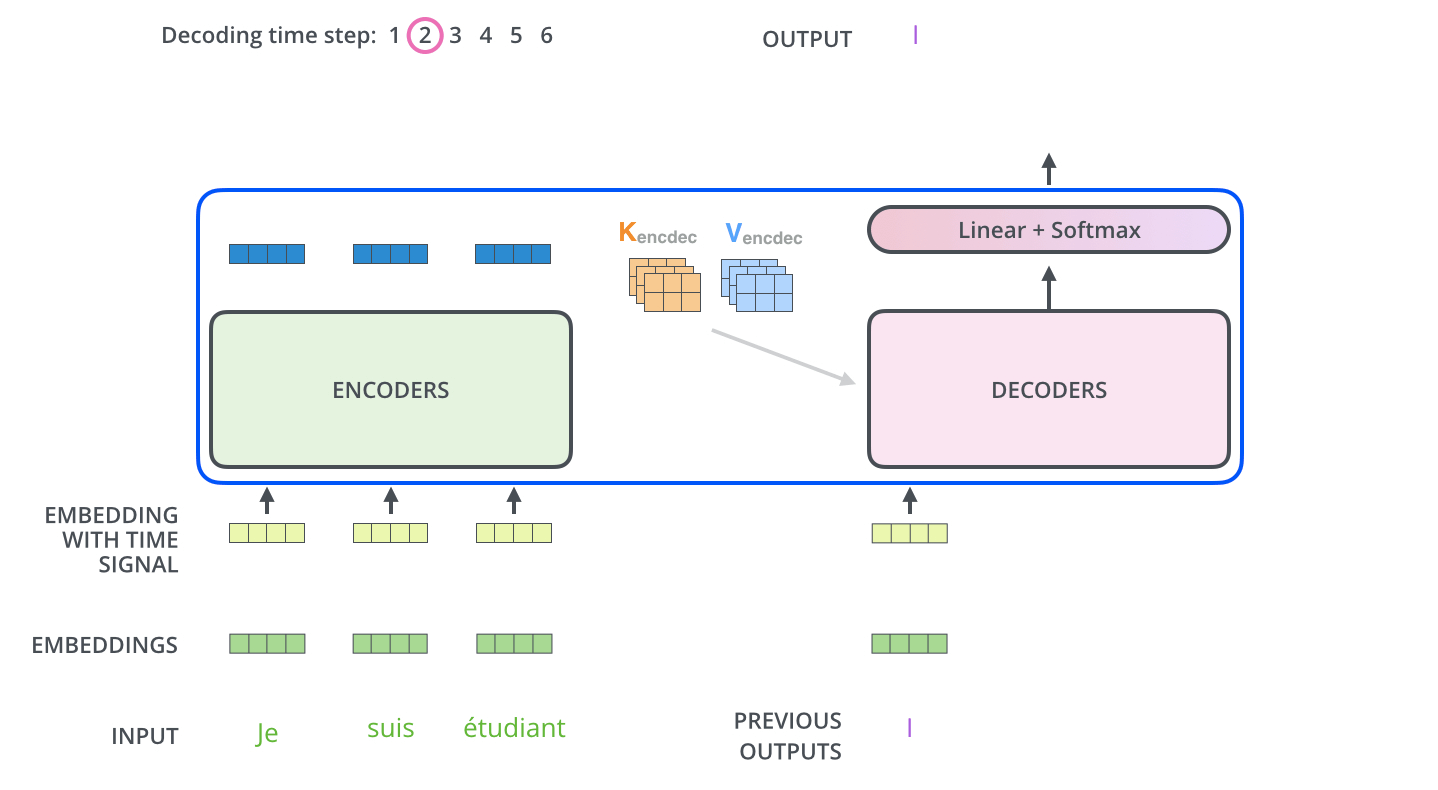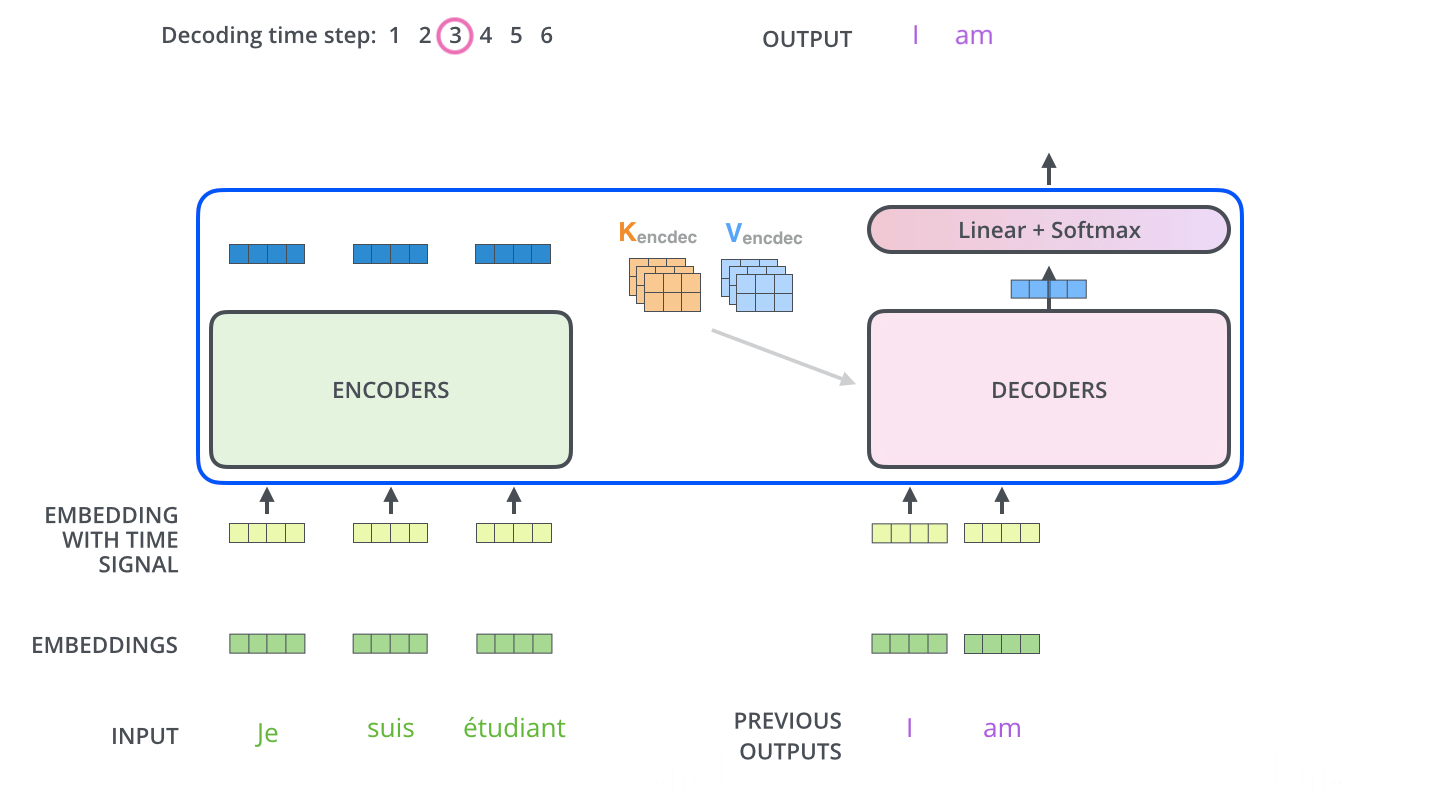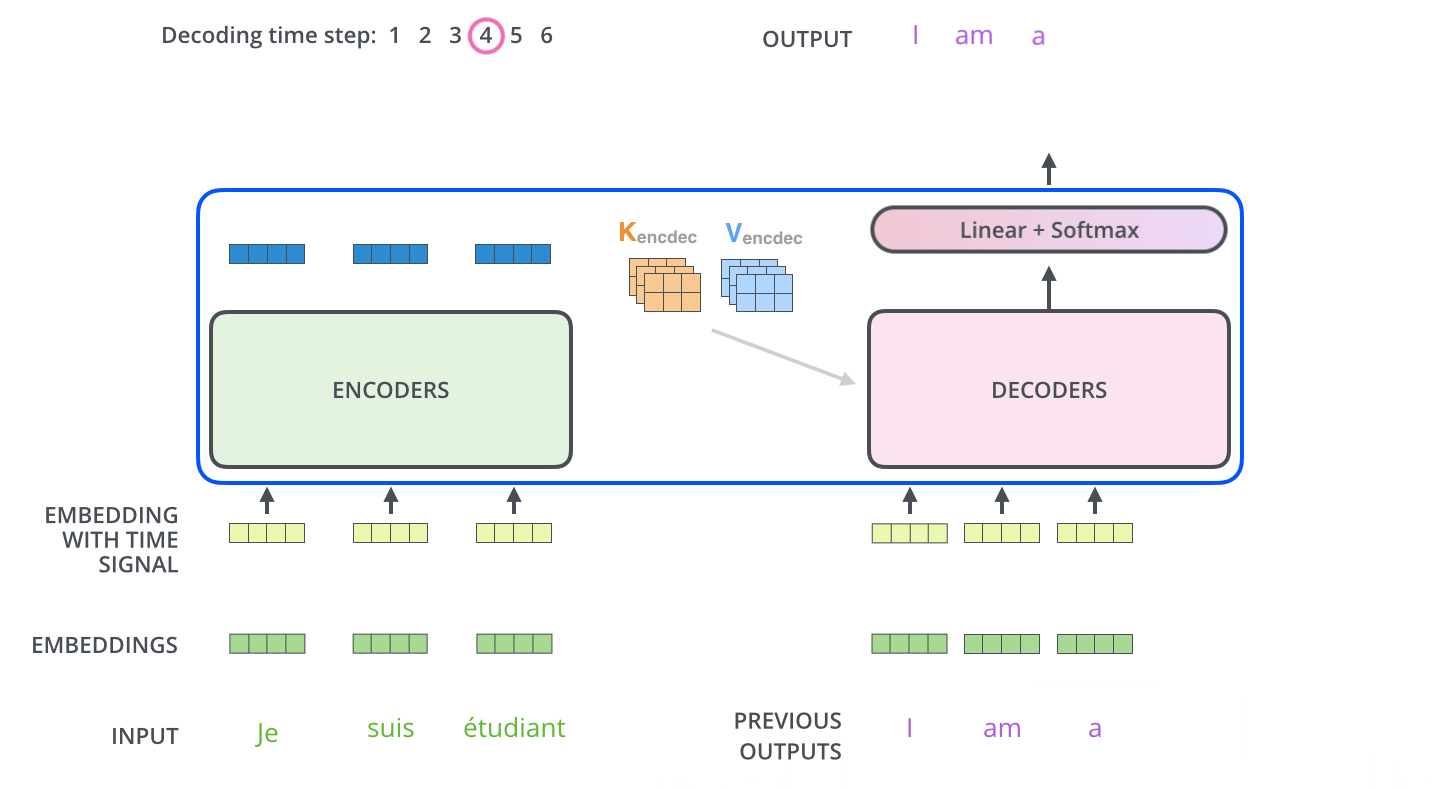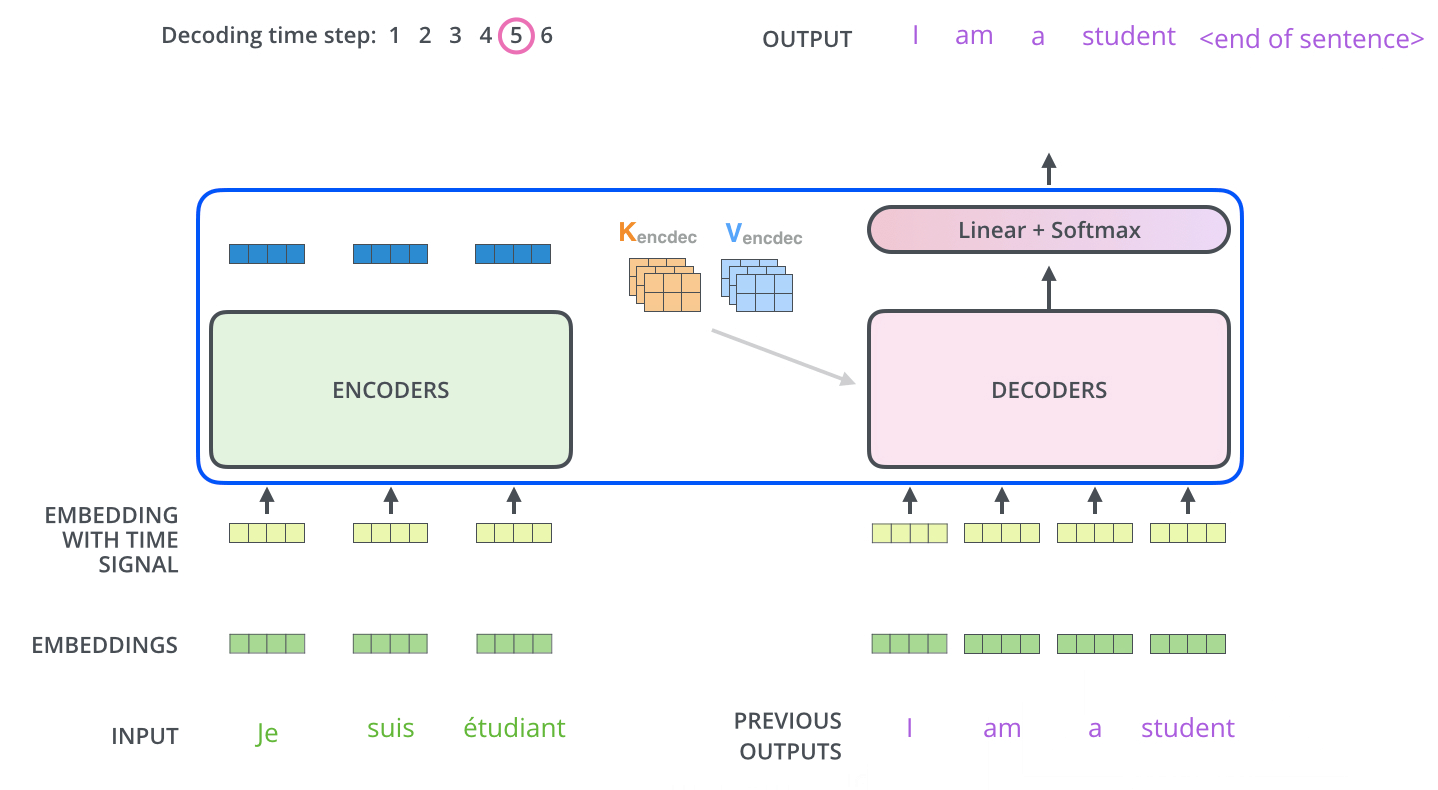
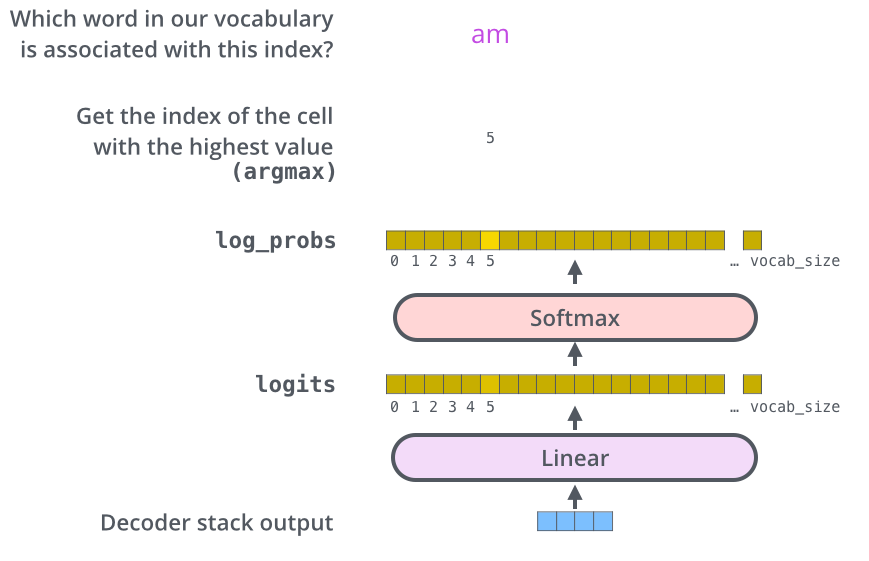
麵粉、砂糖、水、植物油為主，其它成份則視做法及口感需求而有不同。餅乾之所以會出現螺旋線，這是由於兩種顏色的麵糰桿成皮狀，再將彼此疊合而捲成柱狀，以刀切割成每一片厚度相當的餅乾，就可以看出每一片餅乾都帶有螺旋線，經過烘烤後成形，即可食用。
維基百科《螺仔餅》

我先承認我真的沒梗，引言就找這個了XD

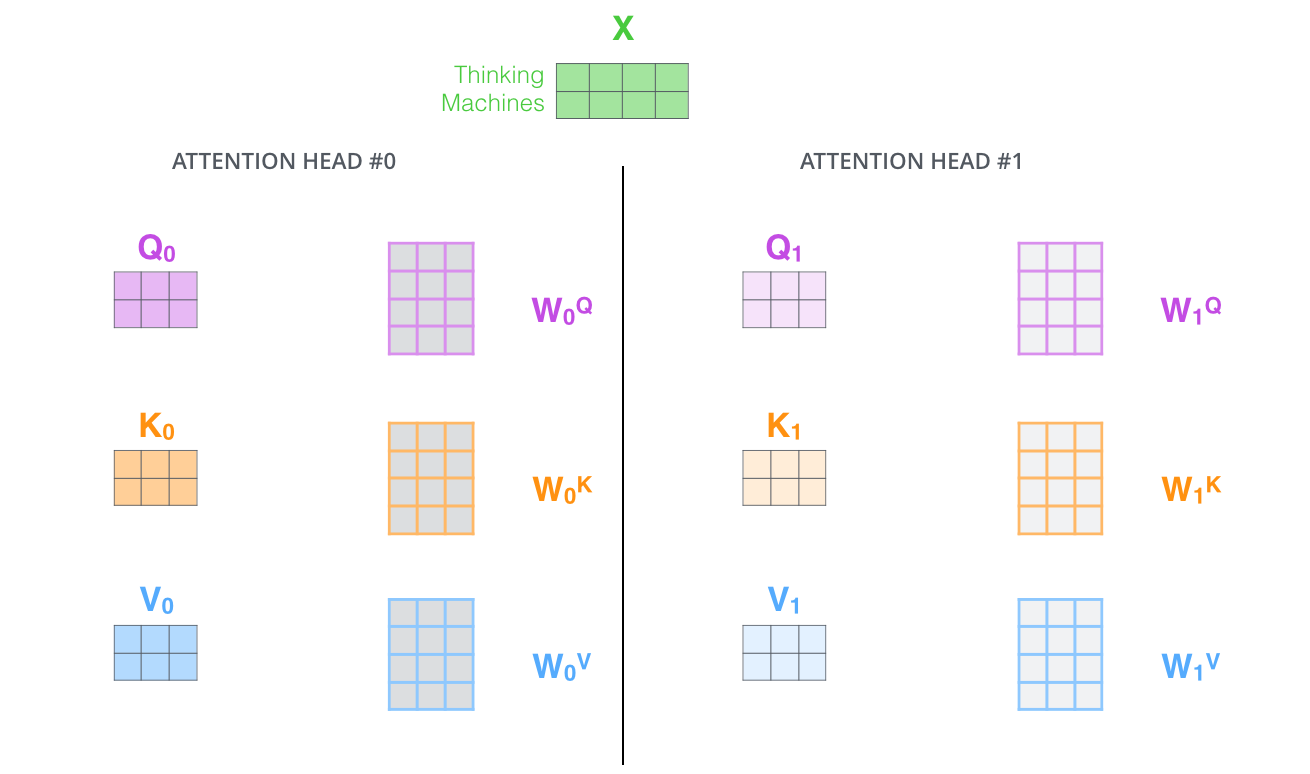
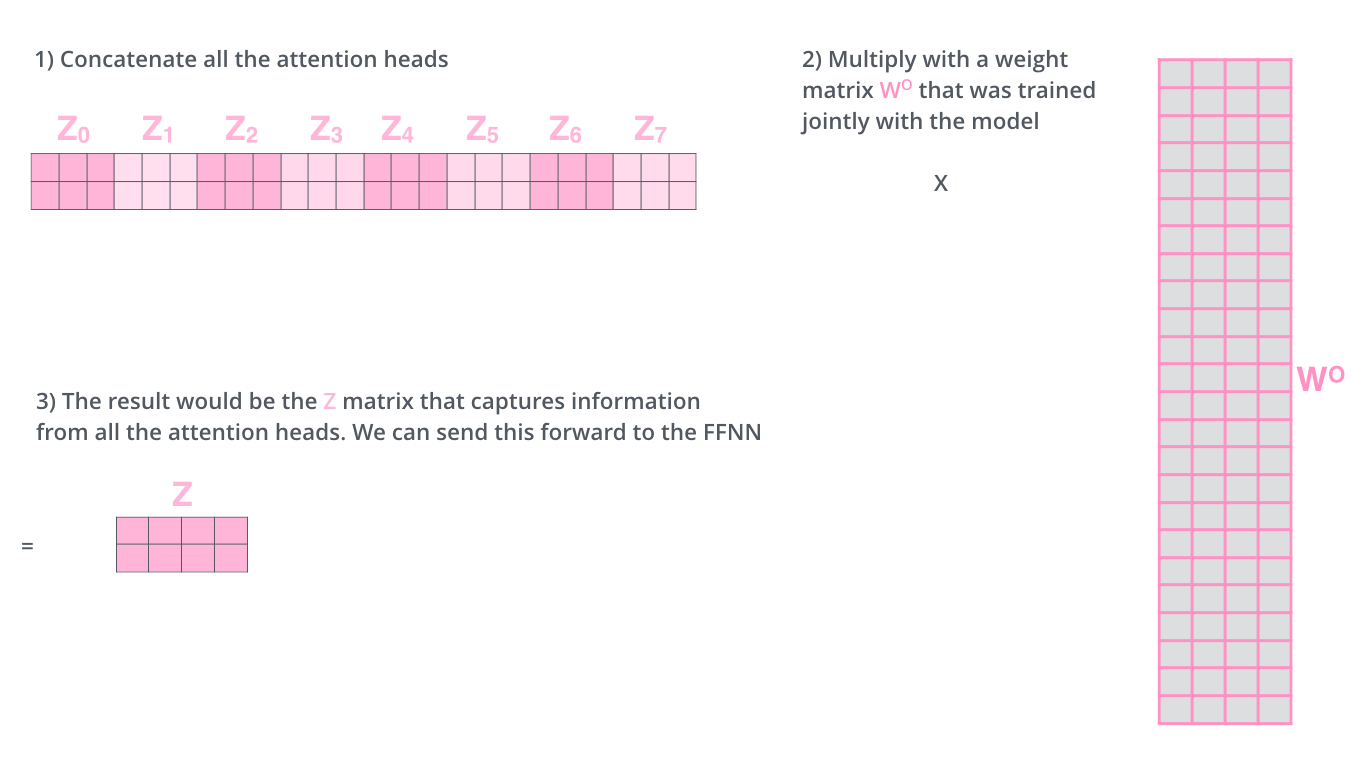
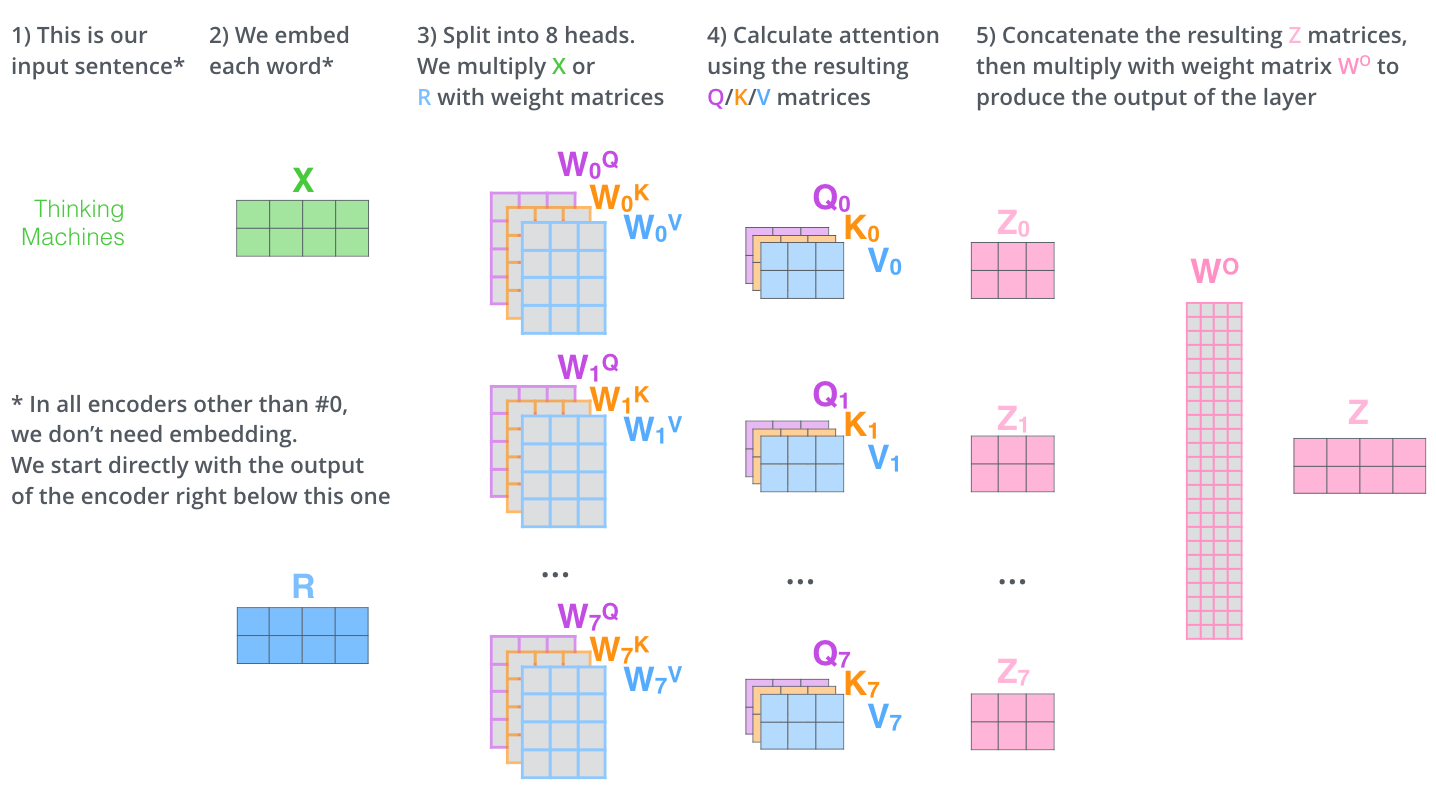
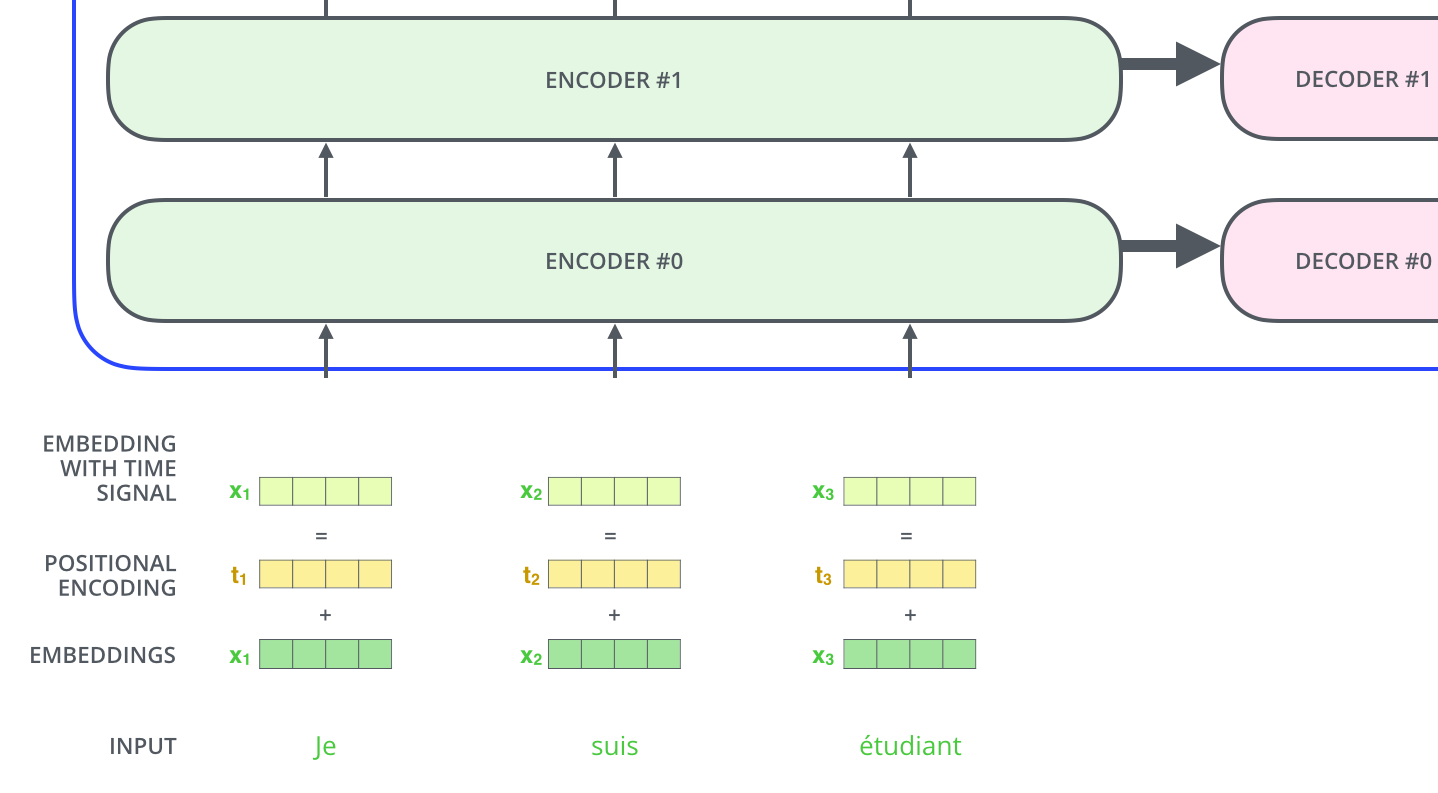
昨天我們講到了貝氏分類器，希望大家都有稍微理解機器學習模型大概會是以什麼方式呈現。我們在進入羅吉斯回歸的模型之前，先來回顧一下所謂的機率性機器學習分類器（probabilistic machine learning classifier）的大致組成吧，其實幾乎所有的機器學習模型都是依循這樣的模式在進行分類的，即便是神經網路也是幾乎雷同，而自然語言處理的模型也不排除在外。

模型架構

• 特徵輸入
  將資料整理成機器學習模型可以理解的形式，首先就是要將這些文字轉換成數字，相信大家都還記得。那其實這種所謂「不同種將文字轉成數字」的方式，也有個專有名詞，稱為特徵工程（feature engineering），特徵工程所得之資料即可作為特徵輸入至模型。
• 換算機率
  完成前面的特徵工程之後，會得到一系列的特徵相關數字，由於這些數字並不是模型的理想輸出（因為記得前面所提模型需要輸出的是分類的機率）所以會經過一系列的數學運算過後，得到最後為0~1之間的機率呈現。
• 最大化與正確答案相符的可能性（Log-likelihood & Loss function）
  接著得到的機率有可能也不會是最好的答案，因為我們需要最小化所謂的損失函數，那要最小化的話，可以透過梯度下降的方式來求得最佳解。
  • 損失函數
  • 梯度下降

羅吉斯回歸

特徵輸入

在自然語言處理的領域中，除了可以透過直覺來判斷文本中可能的特徵之外，不同領域的文本也會有他們各自的特徵（比如說，前一陣子很有名的霸社，或者是將官首文化中的文本，可能就會有屬於其次文化的特殊語言特徵）；另外，近期流行的自然語言處理方式，也會透過先前所說的 Word embedding 的方式作為特徵加入BERT語言模型中。

利用特徵計算原始分數

經過特徵工程之後，我們會得到一串數字（或是向量vector）羅吉斯回歸的第一步，就是先將這些向量x與權重 w（weight）進行內積（dot product）是不是又出現另外一個熟悉的名詞？ ，內積過後得到的數字再加上 b （bias term, a.k.a intercept），這是為了避免有些過度表現的特徵影響了模型的判斷。

我會稱這段過程為計算原始分數。現在說考學測應該還不會暴露年齡吧？你可以這麼理解，我們計算的這個原始分數代表文章是正面或是負面的可能「程度」，就像是學測考完都會有一個「原始分數」。但這個所謂的程度或是原始分數，不是我們想要的結果，對吧？因為我們想要的是這個文本的可能是正面或是負面的「機率」是多少，就像是我們想要知道學測的「級分」，因為「級分」的高低才真正代表表現的好壞。為了要讓模型輸出機率，會再將這個「原始分數」加入激勵函數（activation function）將輸出數值轉換成機率。

利用激勵函數換算機率

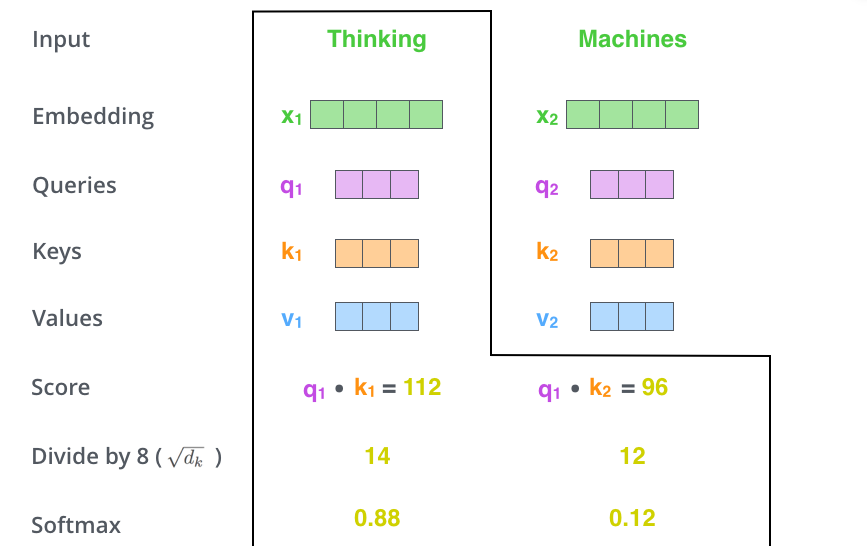
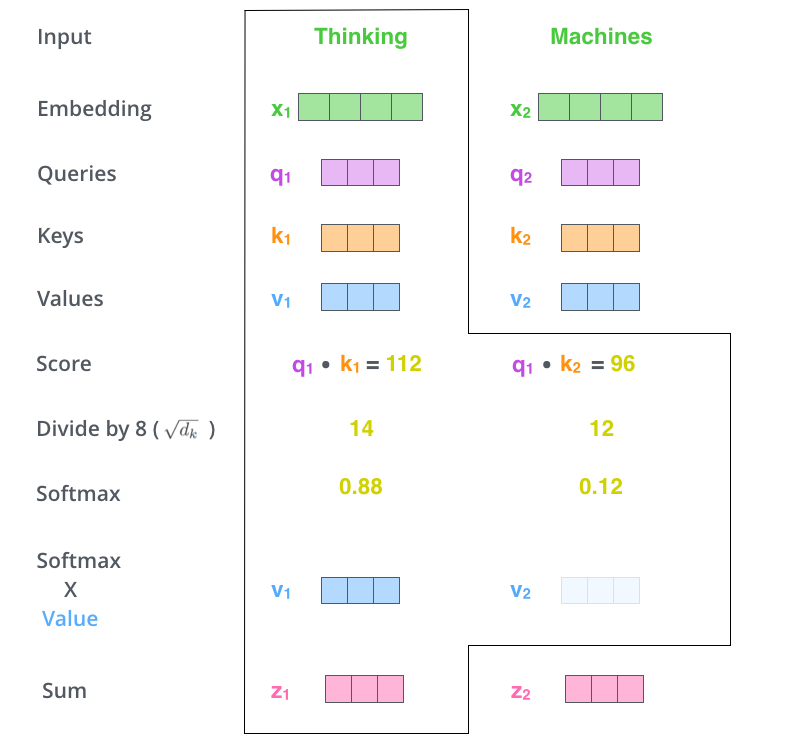
經過前面的計算得到了原始分數之後，我們需要將這段原始分數加入激勵函數來輸出機率。激勵函數有很多種，其中包括今天會介紹的Sigmoid以及softmax，之後會再介紹另外兩種。同樣地，如同先前所說，這些函數各有優缺點，我們在下面來一一討論：

Sigmoid function

Sigmoid函數是最基礎，也是用來處理二元分類最常用的激勵函數。而Sigmoid activation function有幾個好處：

1. Sigmoid可以將「原始分數」壓到[0, 1]之間，正好也是我們所需要的機率形式
2. 在接近0以及接近1的地方，可以發現函數圖形逐漸趨平。這代表若有任何離群值（outlier），Sigmoid函數也可以把他壓縮到接近0或1，但卻又不會超過。
3. 可微分（differentiable），在後續做最佳解時會是一個有利的工具。

softmax function

softmax跟Sigmoid不同的地方在於，這是做多元分類時常用的激勵函數，只是差別在於前者只會給一個機率，而softmax則是會給每個標籤相對應機率，然後加總起來都會等於1。

所以假如說加入「原始分數」，就會是這樣的結果。

最大化與正確答案相符的可能性

前面你可能會發現，咦？那權重是怎麼來的？這就要先從Loss function開始講起：

損失函數（loss function）

損失函數其實就是為了要評估實際答案跟預測答案之間的差距，而要找出這段差距，首先要先進行條件最大機率估算（conditional maximum likelihood estimation），聽起來很複雜，但其實就是要將預測正確的可能性最大化，也就是所謂的log-likelihood。而權重就會在每一次的計算過程中不斷調整，直到找到最佳解。在這邊不會有複雜的數學推演，我只會簡單介紹計算的邏輯。

這裡是一個最大化的最佳解問題。那為了將它變成損失函數，也就是最小化的最佳解問題，在這裡會乘上一個負號

梯度下降

那要解這個最小化問題，在這邊會使用的方法就是梯度下降（gradient descent）。

這名字聽起來好像很可怕，用手算確實可怕，回想我大學在資管系修作業研究的辛酸血淚史（一抹淚），簡單來說，梯度下降法是一種找出最小化最佳解的一種演算法，意味著找出在函數空間中，斜率（slope）往上升程度最大的方向，並往這個方向的反方向前進。是不是不知道我在講什麼？我們馬上來看看一維簡化圖。

首先我們可以先對 w1 微分（這就是為什麼可微分很重要），找出在w1這個點的切線斜率是正亦或是負。若是正（切線方向為/）則代表應該要往左前進。而圖中 w1 的斜率是負的（切線方向為\），所以方向則是往右，方能找到最佳最小值。

但實務上不可能會有這種只有一維的資料吧！所以事實上函數圖形長得會像這樣：

我自己是覺得很像螺仔餅啦，不覺得嗎？我也是去查知道這餅乾的正式名稱

圖片來源：TVBS

那因為 logistic regression 是一個凸函數（convex），而凸函數只會有一個最小值，所以 logistic regression 一定有解。但神經網路不是凸函數（non-convex），所以在進行梯度下降時，就有可能困在同一個地方出不來，因此找不到最佳解。

問題與討論

最後來比較看看貝氏分類模型跟羅吉斯回歸模型。首先，貝氏分類模型過度強調事件的獨立性，而這代表每個輸入的特徵都是獨立的。 這會有什麼問題？假如我們輸入了兩次一模一樣的特徵，貝氏分類會將其視為兩個 完全不同 的特徵，並將這些特徵彼此相乘，最後結果導致模型過度側重這個特徵。但相對的，羅吉斯回歸就不會有這個問題，因為權重會依照特徵進行調整，將權重分配到高度相關的特徵。

但這就代表貝氏分類一無是處嗎？倒也不然。貝氏分類在處理少量資料時，就可以有非常好的表現。且貝氏分類器簡單，訓練速度較快，因此貝氏分類器也是輸人不輸陣的喔！

這裡就再次回應先前所說，沒有什麼最好的方法，只有最適合的方法。最重要的，是了解需求後，找出最適合任務的處理方式，才是最重要的！

好，今天講到這裡，明天要進入深度學習的領域囉！

資料與圖片來源：
Speech and Language Processing